Convexité
Les fonctions considérées ici sont des fonctions à valeurs réelles.
Une partie
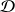du plan est convexe si pour tous points
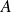et
de
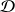, le segment
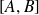est contenu dans
.
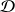C'est équivalent à dire que, pour tout
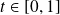, le barycentre de
et
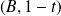appartient à
.
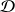Définition :
Une fonction
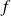est convexe sur un intervalle
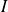si :
.
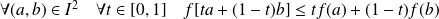Interprétation géométrique : La courbe représentative de
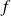est en dessous de ses cordes.
L'ensemble
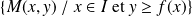des points du plan situés au dessus de la courbe est convexe.
Définition :
Une fonction
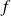est concave sur un intervalle
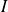si :
.
Interprétation géométrique : La courbe représentative de
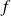est au dessus de ses cordes.
La fonction
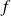est concave sur l'intervalle
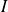si et seulement si la fonction
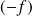est convexe sur
.
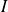L'ensemble
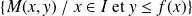des points du plan situés en dessous de la courbe est convexe.
Fondamental :
Inégalités de convexité
Soit
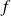une fonction définie sur un intervalle
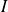de
.
Alors, pour tout
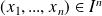et tout
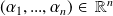tels que
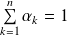, on a :
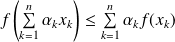si
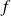est convexe sur
.
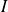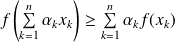si
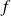est concave sur
.
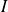Si la somme des coefficients
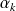n'est pas égale à
, on peut s'y ramener en prenant :
.
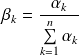Fondamental :
Cas des fonctions dérivables une fois
Soit
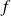une fonction dérivable sur un intervalle
.
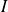La fonction
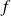est convexe sur
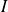si et seulement si sa dérivée
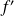est croissante sur
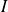.La courbe représentative de
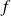est au dessus de toutes ses tangentes.La fonction
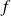est concave sur
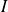si et seulement si sa dérivée
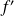est décroissante sur
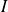.La courbe représentative de
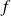est en dessous de toutes ses tangentes.
Fondamental :
Cas des fonctions dérivables deux fois
Soit
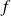une fonction dérivable deux fois sur un intervalle
.
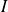La fonction
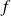est convexe sur
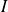si et seulement si
.La fonction
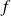est concave sur
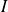si et seulement si
.
Définition :
Un point d'inflexion est un point où la courbe traverse sa tangente.
Si la fonction
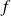est dérivable deux fois sur l'intervalle
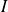, le point
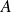d'abscisse
est un point d'inflexion de la courbe si et seulement si la dérivée
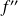s'annule en
en changeant de signe.
