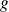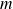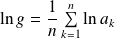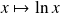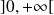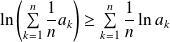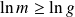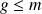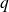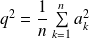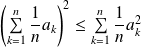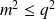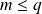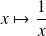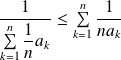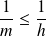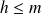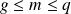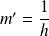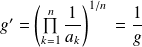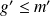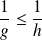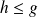Exo 13
Commencez par chercher à résoudre l'exercice par vous-même.
Si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
Etant donnés des réels
, ...,
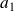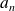strictement positifs, on définit :
leur moyenne arithmétique
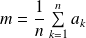.leur moyenne géométrique
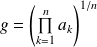.leur moyenne quadratique
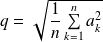.leur moyenne harmonique
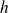telle que
.
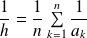