Exo 2
Commencez par chercher à résoudre l'exercice par vous-même.
Si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
Soit
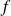la fonction définie sur
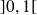par :
.
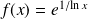Question
Démontrer que la fonction
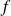est prolongeable par continuité en
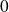et en
, et étudier la dérivabilité de ce prolongement en
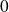et en
.
Déterminez les limites en
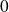et en
de la fonction
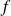et de son taux d'accroissement.
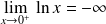. Donc :
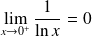. Donc :
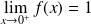. La limite est finie.
Conclusion : La fonction
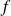est prolongeable par continuité en
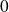en posant :
.
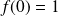Et :
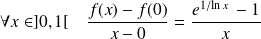. Or :
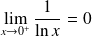, donc :
.
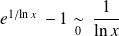Donc :
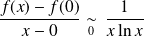. Or :
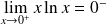. Donc :
.
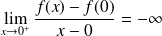Conclusion : Le prolongement de
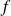n'est pas dérivable en
.
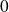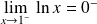. Donc :
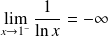. Donc :
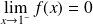. La limite est finie.
Conclusion : La fonction
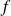est prolongeable par continuité en
en posant :
.
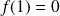Et :
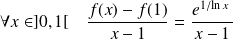. Donc :
.
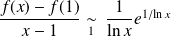Or :
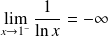, donc :
.
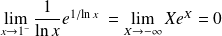Donc :
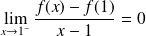. La limite est finie.
Conclusion : Le prolongement de
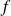est dérivable en
et
.
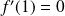La courbe représentative de
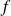admet au point
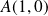une tangente horizontale et au point
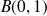une tangente verticale.
