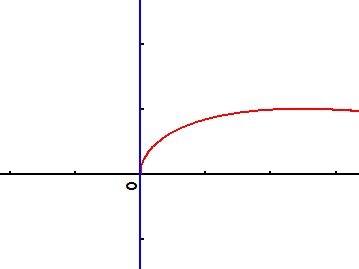
Exo 1
Commencez par chercher à résoudre l'exercice par vous-même.
Si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
Les questions sont indépendantes.
Question
Etudier la dérivabilité en
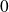de la fonction
:
.
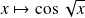Déterminez la limite en
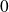du taux d'accroissement de la fonction.
La fonction
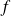est définie sur
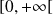. Donc il s'agit de dérivabilité à droite.
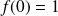, donc :
.
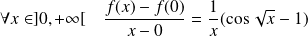Or :
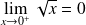. Donc :
.
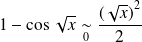Donc :
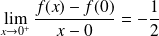. La limite est finie.
Conclusion : La fonction
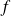est dérivable en
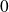et
.
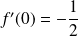La courbe représentative de
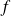admet au point
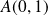une tangente d'équation :
.
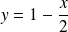Question
Etudier la dérivabilité en
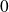de la fonction
:
.
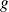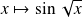Déterminez la limite en
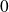du taux d'accroissement de la fonction.
La fonction
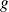est définie sur
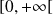. Donc il s'agit de dérivabilité à droite.
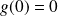, donc :
.
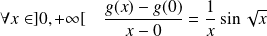Or :
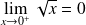. Donc :
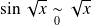. Donc :
.
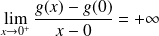Conclusion : La fonction
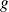n'est pas dérivable en
.
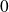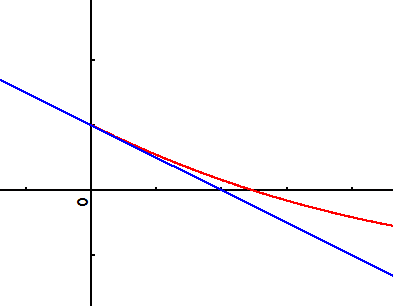
La courbe représentative de la fonction
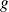admet au point
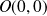une tangente verticale.
