Exo 15
Commencez par chercher à résoudre l'exercice par vous-même.
Si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
Soit
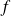une fonction continue sur
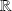qui admet des limites finies en
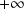et en
.
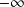Question
Démontrer que la fonction
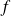est uniformément continue sur
.
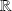Utilisez les définitions des limites à l'infini et la continuité uniforme de
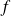sur un segment.
Soit
.
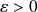On suppose que :
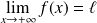. Donc :
.
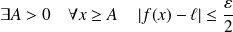Donc :
.
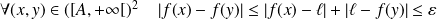De même, si
:
.
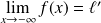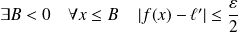Donc :
.
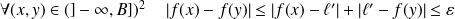De plus,
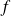est continue sur le segment
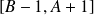, donc uniformément continue.
Donc :
.
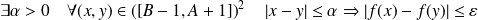Soit
et
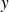deux réels tels que :
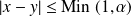. Donc :
.
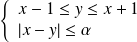Si
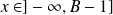, alors
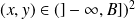, donc :
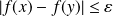.Si
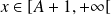, alors
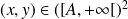, donc :
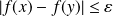.Si
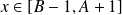, alors
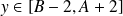, donc il y a trois cas :soit
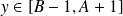, donc
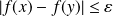puisque
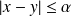.soit
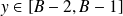et donc
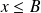, donc
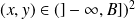, donc :
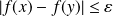.soit
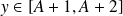et donc
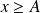, donc
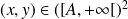, donc :
.
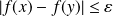Donc :
.
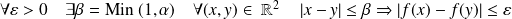Conclusion : La fonction
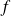est uniformément continue sur
.
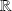