Continuité uniforme
Soit
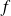une fonction définie sur un intervalle
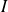de
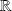, et à valeurs réelles ou complexes.
Rappel : La fonction
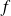est continue sur l'intervalle
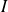si :
.
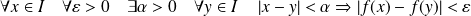Le réel
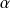dépend de
et de
.
Définition :
La fonction
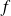est uniformément continue sur l'intervalle
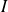si :
.
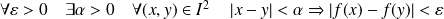Le réel
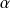est alors indépendant de
. Il ne dépend que de
.
Exemple :
Par exemple, démontrer que la fonction sinus est uniformément continue sur
.
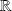Pour montrer la continuité uniforme, on a utilisé la majoration de
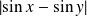par
.
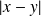On peut généraliser.
Définition :
Une fonction est lipschitzienne sur un intervalle
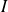s'il existe un réel
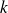tel que :
.
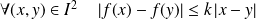On dira que la fonction est
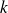- lipschitzienne sur l'intervalle
.
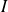Par exemple, la fonction sinus est
- lipschitzienne sur
.
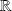Fondamental :
Toute fonction lipschitzienne sur un intervalle
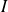est uniformément continue sur
.
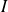La continuité uniforme est une propriété plus forte que la continuité.
Fondamental :
Toute fonction uniformément continue sur un intervalle
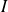est continue sur
.
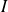Mais la réciproque est fausse.
Exemple :
Par exemple, démontrer que la fonction
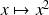est continue sur
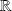mais pas uniformément continue.
Par contre, sur un segment, il y a équivalence entre les deux propriétés.
Fondamental :
Toute fonction continue sur un segment est uniformément continue sur ce segment.
