Exo 12
Commencez par chercher à résoudre l'exercice par vous-même.
Si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
Les questions sont indépendantes.
Question
Résoudre l'équation :
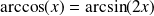 .
.
Introduisez le réel
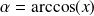 et calculez
et calculez
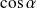 et
et
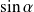 .
.
L'équation est définie si et seulement si
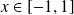 et
et
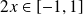 , donc sur
, donc sur
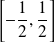 .
.
Soit
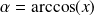 . Donc :
. Donc :
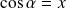 et
et
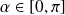 .
.
Soit
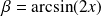 . Donc :
. Donc :
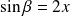 et
et
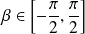 .
.
Donc
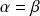 si et seulement si
si et seulement si
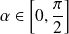 et
et
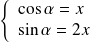 . Or :
. Or :
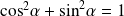 .
.
Donc, si
 est solution de l'équation, alors :
est solution de l'équation, alors :
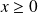 et
et
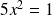 , donc :
, donc :
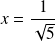 .
.
Réciproquement, si
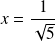 , alors :
, alors :
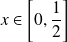 , donc
, donc
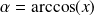 appartient à
appartient à
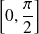 .
.
Donc :
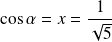 et
et
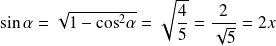 .
.
Or :
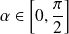 , donc :
, donc :
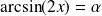 . Donc :
. Donc :
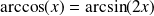 .
.
Conclusion : L'équation
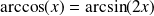 a une unique solution :
a une unique solution :
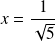 .
.
Question
A quelles conditions sur
 ,
,
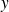 et
et
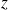 a-t-on :
a-t-on :
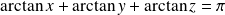 ?
?
Introduisez les réels
 ,
,
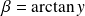 et
et
 .
.
Et cherchez à quelle condition :
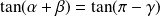 .
.
La relation est définie pour tous les réels
 ,
,
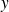 et
et
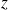 .
.
Les réels
 ,
,
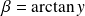 et
et
 appartiennent à
appartiennent à
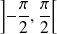 .
.
On a :
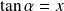 ,
,
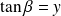 et
et
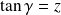 .
.
La relation équivaut à :
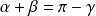 . Or :
. Or :
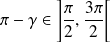 et
et
 .
.
Donc il faut que
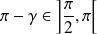 , donc il faut que
, donc il faut que
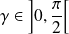 , donc que
, donc que
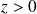 .
.
Or
 ,
,
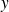 et
et
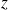 jouent des rôles symétriques. Donc il faut que :
jouent des rôles symétriques. Donc il faut que :
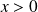 ,
,
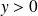 et
et
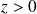 .
.
La fonction tangente est strictement croissante, donc injective sur
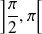 .
.
Donc :
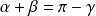 équivaut à :
équivaut à :
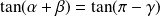 .
.
Or :
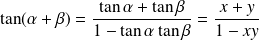 et :
et :
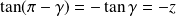 .
.
Donc il faut que :
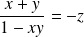 , donc que :
, donc que :
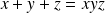 .
.
Réciproquement, on suppose que
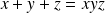 avec
avec
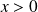 ,
,
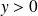 et
et
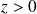 .
.
Donc
 ,
,
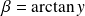 et
et
 appartiennent à
appartiennent à
 .
.
Et :
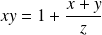 , donc :
, donc :
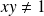 . Donc :
. Donc :
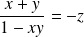 .
.
Donc :
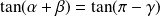 , donc
, donc
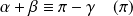 , donc :
, donc :
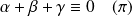 .
.
Or :
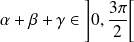 . Donc :
. Donc :
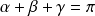 .
.
Donc :
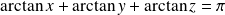 .
.
Conclusion : La relation
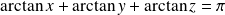 est vérifiée si et seulement si
est vérifiée si et seulement si
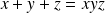 avec
avec
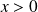 ,
,
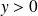 et
et
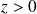 .
.
Question
Démontrer que la série
 est convergente et calculer sa somme.
est convergente et calculer sa somme.
Par récurrence, calculez la somme partielle d'ordre
 de la série en fonction de
de la série en fonction de
 .
.
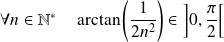 . Or :
. Or :
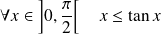 .
.
Donc :
 . Or la série
. Or la série
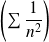 est une série de Riemann convergente (
est une série de Riemann convergente (
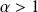 ).
).
Donc la série
 est à termes positifs et majorée par une série convergente, donc elle converge.
est à termes positifs et majorée par une série convergente, donc elle converge.
Soit :
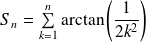 .
.
Donc :
 , et donc :
, et donc :
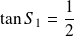 .
.
Et :
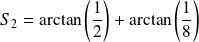 , donc :
, donc :
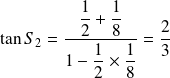 .
.
On conjecture que :
 et on le démontre par récurrence.
et on le démontre par récurrence.
Initialisation : Elle est déjà faite pour
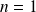 (et même pour
(et même pour
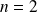 ).
).
Hérédité : Soit
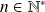 tel que :
tel que :
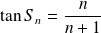 .
.
 . Donc :
. Donc :
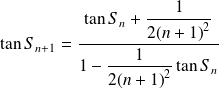 .
.
Donc :
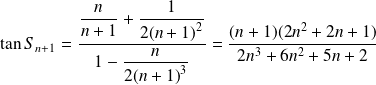 .
.
Or :
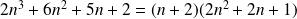 . Donc :
. Donc :
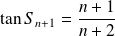 .
.
Conclusion :
 .
.
De plus :
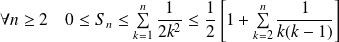 . Or :
. Or :
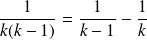 .
.
Donc :
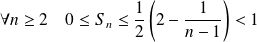 , donc :
, donc :
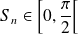 et
et
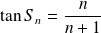 .
.
Donc :
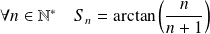 . Donc :
. Donc :
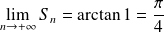 .
.
Conclusion : La série
 est convergente et
est convergente et
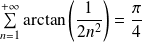 .
.





