Bijectivité
Dans ce qui suit, les fonctions sont à valeurs réelles.
Fondamental :
Théorème de bijection
Si la fonction
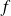est continue et strictement monotone sur un intervalle
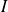, alors
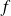est bijective de
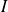dans
.
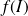Sa fonction réciproque
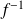est continue et strictement monotone sur
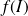, de même sens de variations que
.
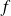Les courbes représentatives des fonctions
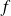et
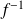sont symétriques par rapport à la droite
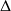d'équation :
.
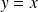Donc, pour tout
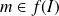, l'équation
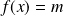admet une unique solution dans
.
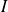Méthode :
Dans la pratique, pour trouver le nombre de solutions d'une équation de la forme
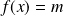dans un intervalle
:
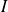on effectue une partition de
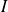en intervalles
, ...,
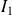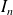sur lesquels la fonction
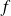est continue et strictement monotone,
on détermine les images
, ...,
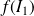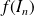de ces intervalles,
sur chaque intervalle
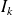, l'équation
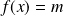admet une solution si et seulement si
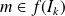, et cette solution est unique.
Remarque : Le sens de variations de la fonction permet ensuite de résoudre les inéquations
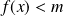ou
.
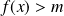Fondamental :
Fonction Arccosinus
La restriction de la fonction cosinus à l'intervalle
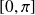est bijective de
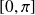dans
.
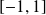Sa réciproque est la fonction Arccosinus :
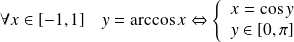
La fonction Arccosinus est définie, continue et strictement décroissante sur l'intervalle
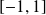, à valeurs dans
.
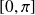En effet, la fonction cosinus est continue et strictement décroissante sur l'intervalle
.
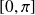Fondamental :
Fonction Arcsinus
La restriction de la fonction sinus à l'intervalle
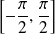est bijective de
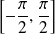dans
.
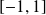Sa réciproque est la fonction Arcsinus :
.
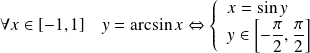La fonction Arcsinus est définie, continue et strictement croissante sur l'intervalle
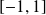, à valeurs dans
.
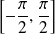En effet, la fonction sinus est continue et strictement croissante sur l'intervalle
.
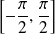Fondamental :
Fonction Arctangente
La restriction de la fonction tangente à l'intervalle
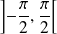est bijective de
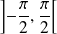dans
.
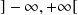Sa réciproque est la fonction Arctangente :
.
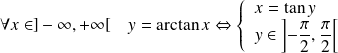La fonction Arctangente est définie, continue et strictement croissante sur l'intervalle
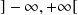, à valeurs dans
.
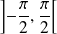En effet, la fonction tangente est continue et strictement croissante sur l'intervalle
.
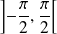