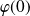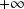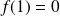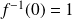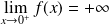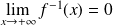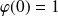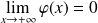Exo 10
Commencez par chercher à résoudre l'exercice par vous-même.
Si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
A tout réel
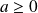 , on associe le polynôme :
, on associe le polynôme :
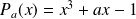 .
.
Question
Montrer que tout polynôme de degré impair admet au moins une racine réelle.
Déterminez l'image de
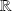 par
par
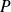 .
.
Tout polynôme
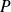 de degré impair et de coefficient dominant
de degré impair et de coefficient dominant
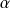 vérifie :
vérifie :
si
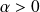 :
:
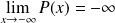 et
et
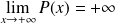 .
.si
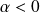 :
:
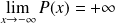 et
et
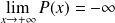 .
.
Donc, puisque
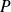 est continu, l'image de
est continu, l'image de
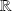 est :
est :
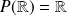 .
.
Donc tout élément de
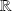 admet au moins un antécédent dans
admet au moins un antécédent dans
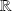 par
par
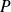 .
.
Conclusion : Tout polynôme de degré impair admet au moins une racine réelle.
Question
Montrer que le polynôme
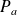 admet une unique racine réelle que l'on note
admet une unique racine réelle que l'on note
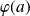 .
.
Etudiez le sens de variations de
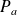 .
.
Le polynôme
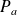 est de degré
est de degré
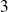 . Il admet donc au moins une racine réelle.
. Il admet donc au moins une racine réelle.
Le polynôme est dérivable :
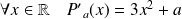 , donc :
, donc :
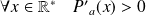 .
.
Donc
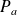 est une fonction strictement croissante sur
est une fonction strictement croissante sur
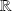 , donc injective.
, donc injective.
Donc tout élément de
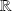 admet au plus un antécédent dans
admet au plus un antécédent dans
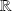 par
par
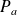 .
.
Conclusion : Le polynôme
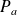 admet une unique racine réelle
admet une unique racine réelle
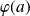 .
.
Question
Montrer que la fonction
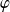 est continue et monotone.
est continue et monotone.
Démontrez que
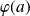 est solution d'une équation de la forme :
est solution d'une équation de la forme :
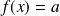 .
.
On peut remarquer que :
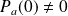 . Donc :
. Donc :
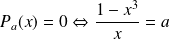 .
.
De plus :
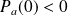 , donc
, donc
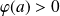 , puisque
, puisque
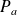 est strictement croissante.
est strictement croissante.
Soit
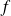 la fonction définie sur
la fonction définie sur
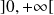 par :
par :
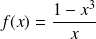 . Donc :
. Donc :
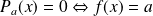 .
.
La fonction
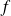 est dérivable sur
est dérivable sur
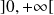 et :
et :
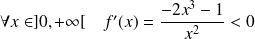 .
.
Donc la fonction
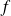 est continue et strictement décroissante sur
est continue et strictement décroissante sur
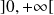 .
.
Donc elle réalise une bijection de
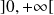 dans
dans
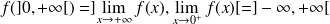 .
.
Donc :
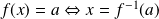 . Donc :
. Donc :
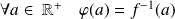 .
.
Donc la fonction
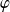 est la restriction de
est la restriction de
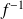 à
à
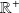 .
.
Conclusion : La fonction
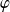 est continue et strictement décroissante sur
est continue et strictement décroissante sur
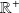 .
.