Exo 11
Commencez par chercher à résoudre l'exercice par vous-même.
Si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
Pour tout
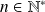 , on note
, on note
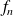 la fonction définie sur
la fonction définie sur
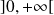 par :
par :
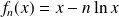 .
.
Question
Démontrer que, pour tout entier
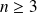 , l'équation
, l'équation
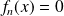 a deux solutions que l'on notera
a deux solutions que l'on notera
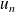 et
et
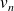 avec :
avec :
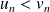 .
.
Etudiez le sens de variations de la fonction
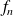 et utilisez le théorème de bijection.
et utilisez le théorème de bijection.
La fonction
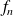 est continue et dérivable sur
est continue et dérivable sur
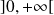 et :
et :
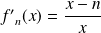 .
.
Donc
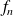 est continue et strictement décroissante sur
est continue et strictement décroissante sur
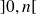 , donc réalise une bijection de
, donc réalise une bijection de
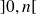 dans
dans
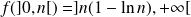 . Or :
. Or :
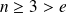 , donc
, donc
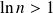 .
.
Donc :
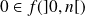 . Donc l'équation
. Donc l'équation
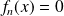 a une unique solution
a une unique solution
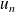 dans
dans
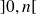 .
.
Et la fonction
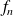 est continue et strictement croissante sur
est continue et strictement croissante sur
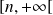 , donc réalise une bijection de
, donc réalise une bijection de
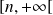 dans
dans
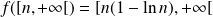 . Or :
. Or :
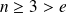 , donc
, donc
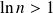 .
.
Donc :
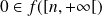 . Donc l'équation
. Donc l'équation
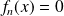 a une unique solution
a une unique solution
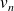 dans
dans
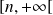 .
.
Conclusion : Pour tout entier
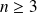 , l'équation
, l'équation
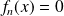 a deux solutions
a deux solutions
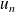 et
et
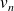 , et
, et
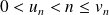 .
.
Question
Démontrer que la suite
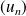 est monotone, qu'elle converge et que :
est monotone, qu'elle converge et que :
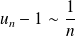 .
.
Démontrez que l'équation
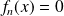 équivaut à une équation de la forme
équivaut à une équation de la forme
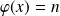 .
.
Démontrez qu'une restriction de la fonction
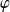 réalise une bijection et utilisez les propriétés de sa réciproque.
réalise une bijection et utilisez les propriétés de sa réciproque.
On peut remarquer que :
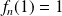 , donc
, donc
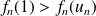 , donc :
, donc :
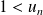 car
car
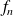 décroît sur
décroît sur
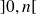 .
.
Sur
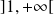 , l'équation
, l'équation
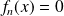 équivaut à
équivaut à
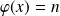 et posant :
et posant :
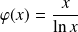 .
.
La fonction
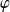 est continue et dérivable sur
est continue et dérivable sur
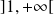 et :
et :
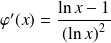 .
.
Donc
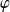 est strictement décroissante sur
est strictement décroissante sur
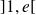 et strictement croissante sur
et strictement croissante sur
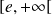 .
.
Donc sa restriction
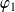 à l'intervalle
à l'intervalle
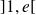 est bijective de
est bijective de
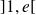 dans
dans
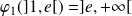 .
.
Or :
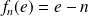 (
(
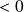 ), donc :
), donc :
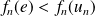 , donc :
, donc :
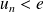 car
car
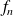 décroît sur
décroît sur
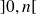 .
.
Donc :
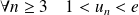 . Donc :
. Donc :
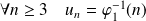 .
.
Or la fonction
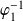 est strictement décroissante et bijective de
est strictement décroissante et bijective de
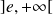 dans
dans
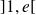 .
.
Donc la suite
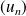 est décroissante et :
est décroissante et :
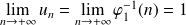 .
.
Donc :
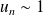 et
et
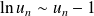 . Or :
. Or :
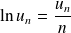 .
.
Conclusion : La suite
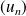 est décroissante, elle converge vers
est décroissante, elle converge vers
 et
et
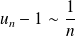 .
.
Question
Démontrer que la suite
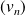 est monotone, qu'elle diverge et que :
est monotone, qu'elle diverge et que :
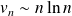 .
.
Utilisez la même méthode que dans la question précédente.
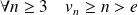 . Donc la suite
. Donc la suite
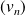 diverge vers
diverge vers
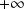 .
.
La restriction
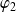 de
de
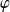 à l'intervalle
à l'intervalle
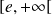 est continue et strictement croissante, donc réalise une bijection de
est continue et strictement croissante, donc réalise une bijection de
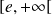 dans
dans
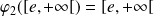 . Et :
. Et :
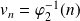 .
.
Or la fonction
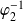 est strictement croissante. Donc la suite
est strictement croissante. Donc la suite
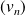 est croissante.
est croissante.
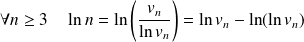 .
.
Or :
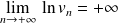 , donc :
, donc :
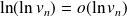 , donc :
, donc :
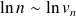 . Or :
. Or :
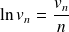 .
.
Conclusion : La suite
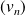 est croissante, elle diverge vers
est croissante, elle diverge vers
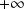 et
et
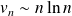 .
.





