Exo 9
Commencez par chercher à résoudre l'exercice par vous-même.
Si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
Soit
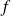la fonction définie par :
.
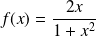Question
Déterminer l'image de
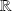par la fonction
.
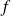Etudiez le sens de variations de la fonction
.
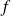On construit une partition de
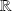en intervalles sur lesquels la fonction
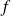est continue et monotone.
La fonction
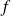est continue et dérivable sur
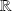. Et :
.
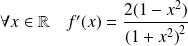Donc
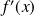est du signe de
.
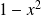Donc
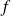est continue et strictement monotone sur les intervalles
,
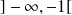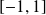et
.
-
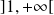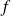est décroissante sur
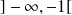, donc :
. -
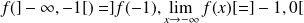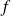est croissante sur
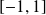, donc :
. -
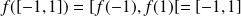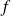est décroissante sur
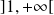, donc :
.
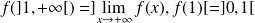Donc :
.
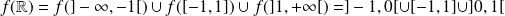Conclusion : L'image de
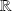par la fonction
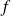est
.
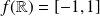Remarque :
L'image par une fonction continue d'un intervalle ouvert non borné peut être un intervalle fermé et borné.
