Exo 8
Commencez par chercher à résoudre l'exercice par vous-même.
Si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
Soit
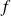une fonction continue et positive sur
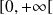qui vérifie :
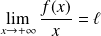avec
.
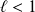Question
Démontrer que la fonction
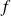admet au moins un point fixe.
Etudiez le signe de la fonction
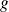définie par :
.
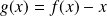Un réel
est un point fixe de
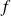si :
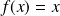, donc si :
.
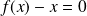La fonction
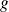définie par :
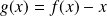est continue sur
.
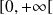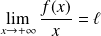, donc :
.
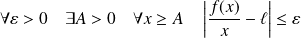En particulier, pour
(
) :
.
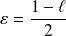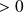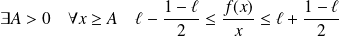Et
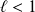, donc :
, donc :
.
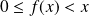Donc :
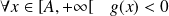. Or :
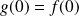, donc :
.
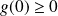La fonction continue
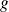prend donc des valeurs positives et négatives sur
.
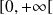Donc la fonction
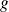s'annule au moins une fois.
Conclusion : La fonction
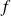admet au moins un point fixe.
