Image d'un intervalle par une fonction continue
Rappel :
Rappel : L'image d'une partie
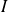 par une application
par une application
 est
est
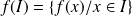 .
.
Donc une équation de la forme
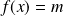 admet des solutions dans
admet des solutions dans
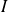 si et seulement si
si et seulement si
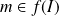 (pas forcément une unique solution).
(pas forcément une unique solution).
Attention :
Dans ce qui suit, les fonctions sont à valeurs réelles.
Fondamental :
Théorème des valeurs intermédiaires
L'image d'un intervalle
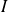 par une fonction
par une fonction
 continue sur
continue sur
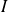 est un intervalle (pas forcément de même nature).
est un intervalle (pas forcément de même nature).
Conséquence : Si
 est continue sur l'intervalle
est continue sur l'intervalle
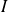 et si
et si
 prend deux valeurs distinctes, elle prend au moins une fois toutes les valeurs intermédiaires.
prend deux valeurs distinctes, elle prend au moins une fois toutes les valeurs intermédiaires.
En particulier, si elle prend une valeur positive et une valeur négative, elle s'annule au moins une fois sur
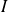 .
.
Fondamental :
L'image d'un segment
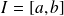 par une fonction
par une fonction
 continue sur
continue sur
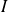 est un segment.
est un segment.
Conséquence : Toute fonction continue sur un segment est bornée, atteint ses bornes et prend au moins une fois toute valeur comprise entre ses bornes.
Si la fonction
 est continue sur un segment
est continue sur un segment
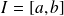 , alors
, alors
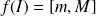 .
.
Donc elle est bornée :
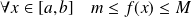 . De plus
. De plus
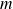 et
et
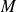 appartiennent à
appartiennent à
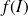 .
.
Donc la fonction
 possède un minimum
possède un minimum
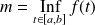 qu'elle atteint : il existe
qu'elle atteint : il existe
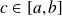 tel que
tel que
 .
.
Et la fonction
 possède un maximum
possède un maximum
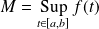 qu'elle atteint : il existe
qu'elle atteint : il existe
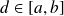 tel que
tel que
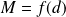 .
.
Et tout réel
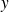 compris entre
compris entre
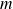 et
et
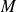 appartient à
appartient à
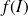 , donc il existe
, donc il existe
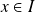 tel que
tel que
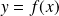 .
.
Remarque : Une fonction
 à valeurs complexes continue sur un segment
à valeurs complexes continue sur un segment
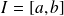 est aussi bornée puisque ses parties réelle et imaginaire sont bornées.
est aussi bornée puisque ses parties réelle et imaginaire sont bornées.
Fondamental :
Cas d'une fonction continue et strictement monotone
Si la fonction
 est continue et strictement monotone sur un intervalle
est continue et strictement monotone sur un intervalle
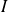 , alors
, alors
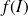 est un intervalle de même nature (ouvert ou fermé) que
est un intervalle de même nature (ouvert ou fermé) que
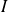 , obtenu en prenant les valeurs de
, obtenu en prenant les valeurs de
 ou les limites de
ou les limites de
 aux bornes de
aux bornes de
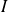 (il faut intervertir les bornes si
(il faut intervertir les bornes si
 est décroissante) :
est décroissante) :
Si
 est continue et strictement croissante sur
est continue et strictement croissante sur
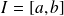 , alors
, alors
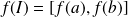 .
.Si
 est continue et strictement décroissante sur
est continue et strictement décroissante sur
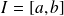 , alors
, alors
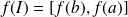 .
.Si
 est continue et strictement croissante sur
est continue et strictement croissante sur
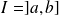 (avec
(avec
 réel ou infini), alors
réel ou infini), alors
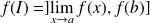 .
.Si
 est continue et strictement décroissante sur
est continue et strictement décroissante sur
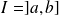 (avec
(avec
 réel ou infini), alors
réel ou infini), alors
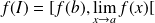 .
.Si
 est continue et strictement croissante sur
est continue et strictement croissante sur
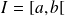 (avec
(avec
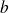 réel ou infini), alors
réel ou infini), alors
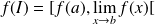 .
.Si
 est continue et strictement décroissante sur
est continue et strictement décroissante sur
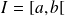 (avec
(avec
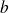 réel ou infini), alors
réel ou infini), alors
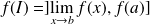 .
.Si
 est continue et strictement croissante sur
est continue et strictement croissante sur
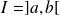 (avec
(avec
 et
et
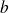 réels ou infinis), alors
réels ou infinis), alors
 .
.Si
 est continue et strictement décroissante sur
est continue et strictement décroissante sur
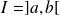 (avec
(avec
 et
et
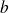 réels ou infinis), alors
réels ou infinis), alors
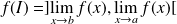 .
.
Dans la pratique, pour déterminer l'image
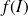 , on partage
, on partage
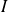 en intervalles sur lesquels la fonction
en intervalles sur lesquels la fonction
 est continue et strictement monotone.
est continue et strictement monotone.





