Exo 3
Commencez par chercher à résoudre l'exercice par vous-même.
Si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
Soit
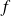 la fonction définie par :
la fonction définie par :
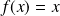 si
si
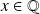 et
et
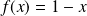 si
si
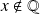 .
.
Question
Démontrez que tout réel
 est limite d'une suite de rationnels et d'une suite d'irrationnels.
est limite d'une suite de rationnels et d'une suite d'irrationnels.
Utilisez les valeurs décimales approchées de
 par défaut et par excès.
par défaut et par excès.
Pour
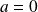 , il suffit de prendre la suite de rationnels
, il suffit de prendre la suite de rationnels
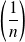 et la suite d'irrationnels extraite de la suite
et la suite d'irrationnels extraite de la suite
 obtenue en supprimant tous les termes où
obtenue en supprimant tous les termes où
 est le carré d'un entier.
est le carré d'un entier.
Soit
 un réel non nul. On note :
un réel non nul. On note :
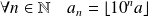 . Donc :
. Donc :
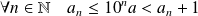 .
.
Donc
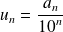 est un rationnel et :
est un rationnel et :
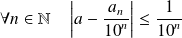 , donc :
, donc :
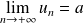 .
.
Conclusion : Il existe une suite de rationnels qui converge vers
 .
.
Si
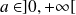 , alors :
, alors :
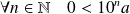 , donc :
, donc :
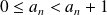 .
.
Si
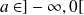 , alors
, alors
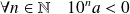 , donc :
, donc :
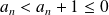 .
.
Donc, dans les deux cas :
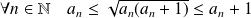 , donc :
, donc :
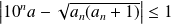 .
.
Or pour tout entier
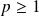 ,
,
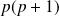 n'est pas le carré d'un entier.
n'est pas le carré d'un entier.
En effet, s'il existait un entier
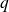 tel que
tel que
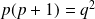 , on aurait
, on aurait
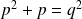 .
.
On aurait donc :
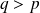 et
et
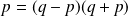 , ce qui est impossible car
, ce qui est impossible car
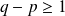 et
et
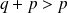 .
.
Et pour tout entier
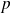 :
:
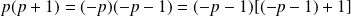 .
.
Donc pour tout entier
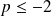 ,
,
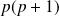 n'est pas le carré d'un entier.
n'est pas le carré d'un entier.
Par contre, pour
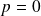 ou
ou
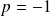 , on a :
, on a :
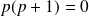 (carré d'entier).
(carré d'entier).
Donc
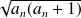 est un irrationnel sauf si
est un irrationnel sauf si
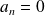 ou
ou
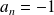 .
.
Or si
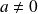 , à partir d'un certain rang, on aura
, à partir d'un certain rang, on aura
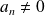 et
et
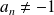 .
.
Donc
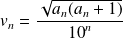 est un irrationnel à partir d'un certain rang.
est un irrationnel à partir d'un certain rang.
Or :
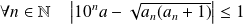 , donc :
, donc :
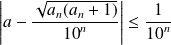 , donc :
, donc :
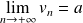 .
.
Conclusion : Il existe une suite d'irrationnels qui converge vers
 .
.
Question
Déterminer en quels points la fonction
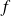 est continue.
est continue.
Etudiez successivement les cas où
 est rationnel et où
est rationnel et où
 est irrationnel.
est irrationnel.
On étudie successivement les cas où
 est rationnel et irrationnel.
est rationnel et irrationnel.
Soit
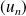 une suite de rationnels et
une suite de rationnels et
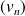 une suite d'irrationnels qui convergent vers
une suite d'irrationnels qui convergent vers
 .
.
Donc, si
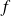 est continue en
est continue en
 , alors :
, alors :
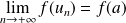 et
et
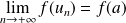 .
.
Soit
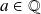 , donc :
, donc :
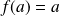 .
.Donc :
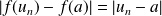 et
et
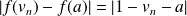 .
.Donc :
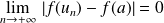 et
et
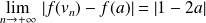 .
.Donc, si
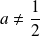 , on n'a pas
, on n'a pas
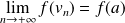 . Donc
. Donc
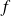 n'est pas continue en
n'est pas continue en
 .
.
Pour
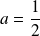 et pour tout réel
et pour tout réel
 rationnel ou pas :
rationnel ou pas :
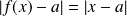 car
car
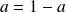 .
.Donc :
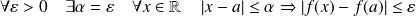 .
.Donc
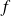 est continue en
est continue en
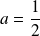 .
.
Soit
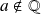 , donc :
, donc :
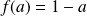 .
. Donc :
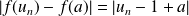 et
et
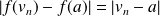 .
.Donc :
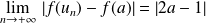 et
et
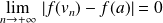 .
.Or
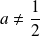 , donc on n'a pas
, donc on n'a pas
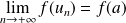 . Donc
. Donc
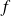 n'est pas continue en
n'est pas continue en
 .
.
Conclusion : La fonction
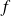 est continue en
est continue en
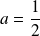 et discontinue en tout
et discontinue en tout
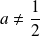 .
.





