Continuité en un point
Dans ce qui suit, les fonctions sont définies sur un intervalle de
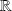et à valeurs réelles ou complexes.
Définition :
Soit
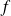une fonction définie sur un intervalle
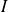et soit
.
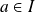La fonction
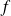est continue en
si :
.
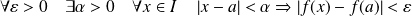Donc la fonction
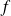est continue en
si elle admet une limite finie en
:
.
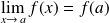Une fonction
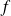à valeurs complexes est continue en
si et seulement si ses parties réelle et imaginaire sont continues en
.
Fondamental :
Fonctions usuelles
Les fonctions polynômes sont continues en tout point
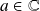.Les fonctions rationnelles sont continues en tout point
de leur ensemble de définition.Les fonctions sinus et cosinus sont continues en tout point
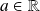.La fonction exponentielle est continue en tout point
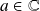.La fonction logarithme népérien est continue en tout point
.
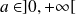Définition :
Une fonction
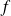est continue à gauche en
si la restriction de
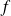à
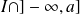est continue en
.Donc
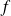est continue à gauche en
si
.
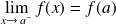Une fonction
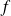est continue à droite en
si la restriction de
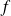à
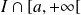est continue en
.Donc
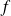est continue à droite en
si
.
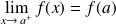Exemple :
Par exemple, la fonction
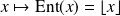(partie entière) est continue en tout réel
non entier.
Elle est continue à droite, mais pas à gauche en tout
.
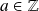Fondamental :
Une fonction
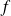définie à gauche et à droite de
est continue en
si et seulement si elle est continue à gauche et à droite de
.
La condition est donc :
.
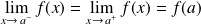Les propriétés viennent des propriétés des limites et sont valables pour la continuité en
, pour la continuité à gauche en
et pour la continuité à droite en
.
Fondamental :
Opérations algébriques
Si la fonction
est continue en
et si
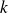est une constante, alors la fonction
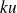est continue en
.Si les fonctions
et
sont continues en
, alors les fonctions
et
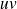sont continues en
.Si les fonctions
et
sont continues en
, alors la fonction
est continue en
si
.
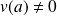Fondamental :
Composition
Si la fonction
à valeurs réelles est continue en
et si la fonction
est continue en
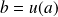, alors la fonction
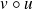est continue en
.
Conséquences : Si la fonction
est continue en
, alors les fonctions
,
,
,
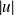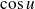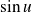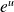sont continues en
.
Si la fonction
est continue en
, alors la fonction
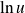est continue en
si
.
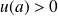Définition :
Une fonction
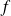définie au voisinage de
, mais pas en
, est prolongeable par continuité en
si elle admet une limite finie
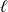en
.
Son prolongement par continuité est la fonction
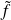continue en
qui est définie sur
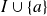par :
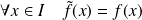et
.
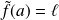