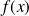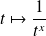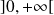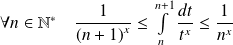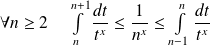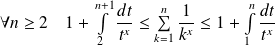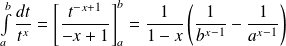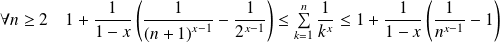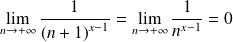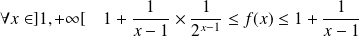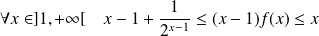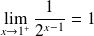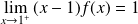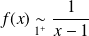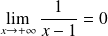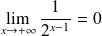Exo 14
Commencez par chercher à résoudre l'exercice par vous-même.
Si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
Soit
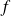la fonction définie sur
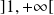par :
.
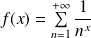Question
Déterminer la limite de la fonction
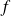en
.
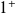Utilisez la monotonie de
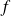pour montrer l'existence d'une limite, puis démontrez qu'elle n'est pas finie.
La série de Riemann
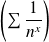converge si et seulement si
.
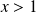Donc la fonction
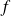est définie sur
.
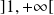Pour tout entier
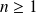, la fonction
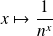est décroissante sur
.
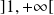Donc la fonction
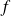est décroissante sur
.
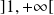Donc elle admet une limite finie ou infinie en
.
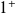Supposons qu'elle admette une limite finie
.
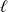Or :
.
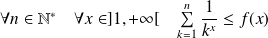Donc, par passage à la limite :
.
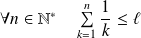Or la série harmonique
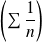est divergente, donc :
.
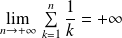On aboutit donc à une contradiction. Donc la limite de
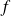n'est pas finie.
Conclusion :
.
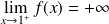Question
Question
Question
Déterminer un équivalent de
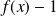en
.
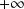Démontrez que la fonction définie par :
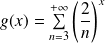a pour limite 0 en
.
.
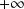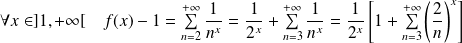On pose :
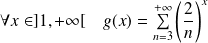et :
.
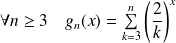Donc :
.
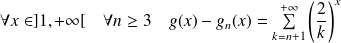Or toutes les fonctions
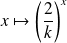sont décroissantes si
.
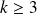Donc :
.
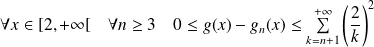Donc :
.
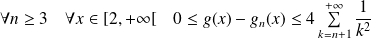Soit
.
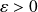La série
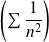est une série de Riemann convergente, donc :
.
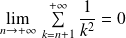Donc il existe un entier
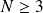tel que :
.
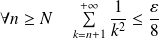Donc :
.
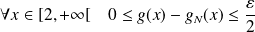Donc :
.
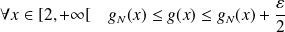Or :
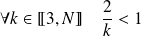, donc :
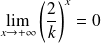. Donc :
.
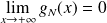Donc :
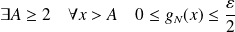, donc :
.
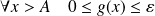Donc :
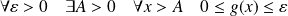. Donc :
.
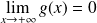Or :
.
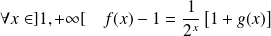Conclusion :
.
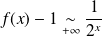