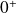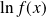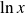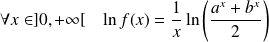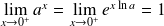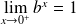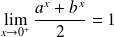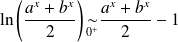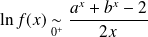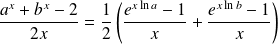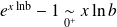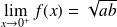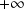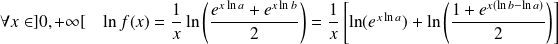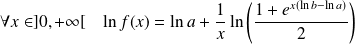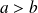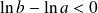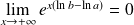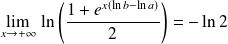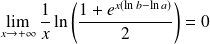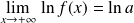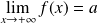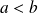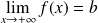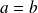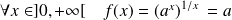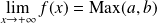Exo 11
Commencez par chercher à résoudre l'exercice par vous-même.
Si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
Soient
 et
et
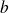 deux réels strictement positifs.
deux réels strictement positifs.
Soit
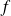 la fonction définie par :
la fonction définie par :
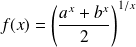 sur
sur
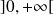 .
.