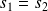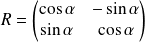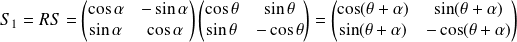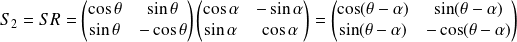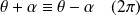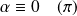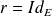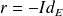Exo 5
Commencez par chercher à résoudre l'exercice par vous-même.
Si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
Soit
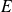 un plan vectoriel euclidien orienté et
un plan vectoriel euclidien orienté et
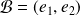 une base orthonormale directe.
une base orthonormale directe.
Soit
 une rotation vectorielle d'angle
une rotation vectorielle d'angle
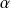 et
et
 une réflexion d'axe
une réflexion d'axe
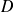 .
.
Question
Démontrer qu'il existe une unique réflexion
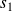 telle que
telle que
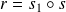 et une unique réflexion
et une unique réflexion
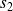 telle que
telle que
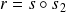 .
.
La réflexion
 est bijective et involutive, donc sa réciproque est :
est bijective et involutive, donc sa réciproque est :
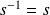 .
.
Donc :
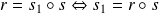 et
et
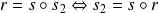 .
.
Or
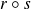 et
et
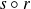 sont composés d'un endomorphisme orthogonal direct et d'un endomorphisme orthogonal indirect, donc sont des endomorphismes orthogonaux indirects, donc des réflexions.
sont composés d'un endomorphisme orthogonal direct et d'un endomorphisme orthogonal indirect, donc sont des endomorphismes orthogonaux indirects, donc des réflexions.
Conclusion : Pour toute rotation
 et toute réflexion
et toute réflexion
 , il existe une unique réflexion
, il existe une unique réflexion
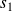 telle que
telle que
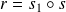 et une unique réflexion
et une unique réflexion
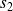 telle que
telle que
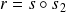 .
.
Question
Question
Est-il possible que les axes
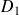 et
et
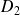 de
de
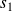 et
et
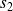 soient orthogonaux ?
soient orthogonaux ?
Déterminez les axes
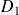 et
et
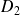 .
.
L'axe
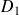 de
de
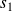 est l'ensemble de ses vecteurs invariants.
est l'ensemble de ses vecteurs invariants.
Donc
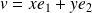 appartient à
appartient à
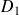 si et seulement si :
si et seulement si :
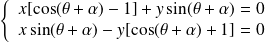 .
.
Or :
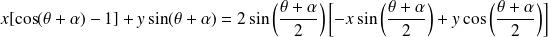 .
.
Et :
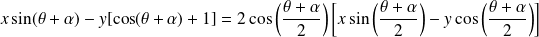 .
.
Or
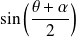 et
et
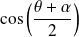 ne sont pas simultanément nuls.
ne sont pas simultanément nuls.
Donc l'axe
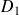 de
de
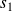 a pour équation :
a pour équation :
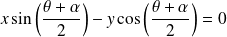 .
.
De même l'axe
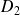 de
de
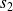 a pour équation :
a pour équation :
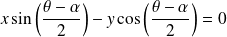 .
.
Donc les axes
 et
et
 de
de
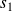 et
et
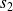 sont orthogonaux si et seulement si les vecteurs
sont orthogonaux si et seulement si les vecteurs
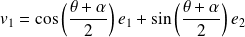 et
et
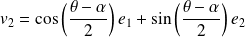 sont orthogonaux.
sont orthogonaux.
Donc
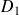 et
et
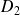 sont orthogonaux si et seulement si :
sont orthogonaux si et seulement si :
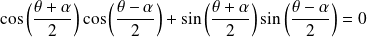 , donc si
, donc si
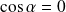 (et donc
(et donc
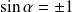 ).
).
Conclusion : Les axes
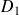 et
et
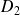 de
de
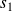 et
et
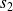 sont orthogonaux si et seulement si
sont orthogonaux si et seulement si
 est la rotation vectorielle d'angle
est la rotation vectorielle d'angle
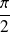 ou
ou
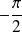 .
.
Question
Soit
 la rotation vectorielle d'angle
la rotation vectorielle d'angle
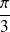 et
et
 la réflexion par rapport à la droite
la réflexion par rapport à la droite
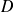 d'équation
d'équation
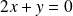 dans
dans
 .
.
Déterminer les axes des réflexions
 et
et
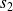 .
.
Déterminez la matrice de
 , puis celles de
, puis celles de
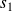 et
et
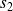 .
.
L'angle de la rotation
 est
est
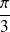 , donc sa matrice dans
, donc sa matrice dans
 est :
est :
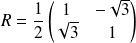 .
.
La matrice de la réflexion
 est de la forme :
est de la forme :
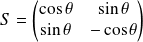 .
.
Le vecteur
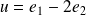 appartient à l'axe de
appartient à l'axe de
 . Donc
. Donc
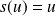 .
.
Donc :
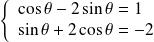 . Donc
. Donc
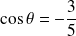 ,
,
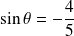 et
et
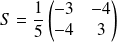 .
.
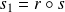 . Donc :
. Donc :
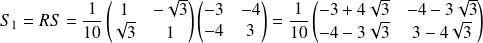 .
.
L'axe
 de
de
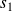 est l'ensemble de ses vecteurs invariants.
est l'ensemble de ses vecteurs invariants.
Donc un vecteur
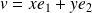 appartient à
appartient à
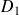 si et seulement si :
si et seulement si :
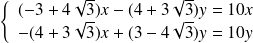 .
.
Conclusion :
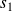 est la réflexion d'axe
est la réflexion d'axe
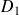 d'équation
d'équation
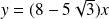 .
.
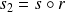 . Donc :
. Donc :
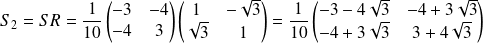 .
.
L'axe
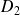 de
de
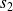 est l'ensemble de ses vecteurs invariants.
est l'ensemble de ses vecteurs invariants.
Donc un vecteur
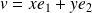 appartient à
appartient à
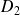 si et seulement si :
si et seulement si :
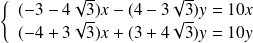 .
.
Conclusion :
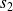 est la réflexion d'axe
est la réflexion d'axe
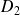 d'équation
d'équation
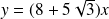 .
.