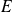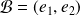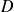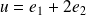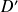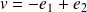Exo 3
Commencez par chercher à résoudre l'exercice par vous-même.
Si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
Soit
Soit
Soit
|  |
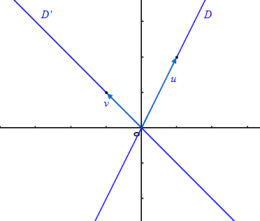Question
Déterminer tous les endomorphismes orthogonaux
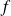tels que :
.
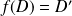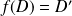si et seulement si les vecteurs
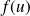et
sont colinéaires.
Soit
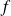un endomorphisme orthogonal.
La matrice de
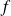dans la base
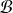est de la forme :
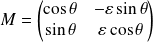avec
.
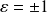Donc :
.
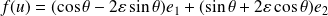Or
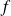est un endomorphisme orthogonal, donc bijectif, donc
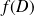est la droite vectorielle engendrée par le vecteur
.
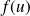Donc
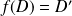si et seulement si les vecteurs
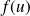et
sont colinéaires.
Or :
.
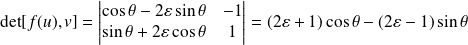Donc
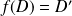si et seulement si
.
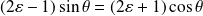Or pour
:
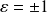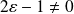. Et si
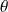est solution, alors :
.
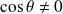Donc
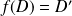si et seulement si
.
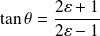Et :
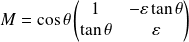. Or :
.
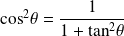Donc, pour
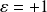, on obtient
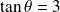et
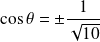, donc :
.
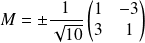Et, pour
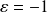, on obtient
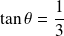et
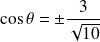, donc :
.
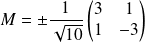On vérifie facilement que ces quatre matrices conviennent.
Conclusion : Il existe quatre endomorphismes orthogonaux
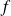tels que
.
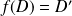Il y a deux rotations vectorielles de matrices
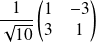et
.
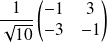Il y a deux réflexions vectorielles de matrices
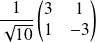et
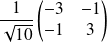
Remarque
Les mesures des angles des rotations vectorielles sont
et
.
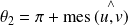Donc l'angle
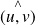a pour mesure
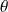tel que :
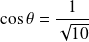et
.
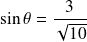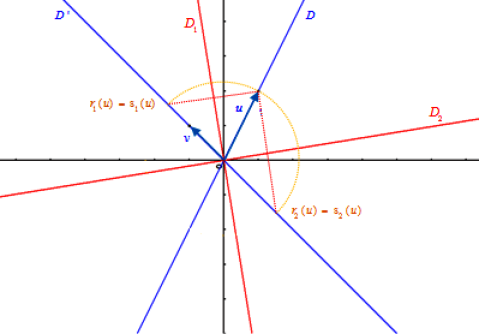
Les axes des réflexions sont les bissectrices de l'angle
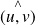(donc orthogonales).
Donc les bissectrices
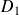et
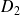de l'angle
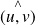ont pour équations :
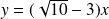et
.
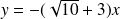