Caractéristiques des endomorphismes orthogonaux en dimension 2
On suppose l'espace vectoriel euclidien
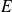orienté et rapporté à une base
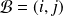orthonormale directe.
Définition :
Etant donnés deux vecteurs unitaires
et
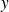, il existe une unique rotation
telle que
.
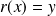Deux couples de vecteurs unitaires
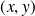et
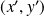sont équivalents s'il existe une rotation
telle que
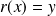et
.
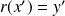L'angle orienté
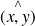des vecteurs unitaires
et
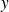est la classe d'équivalence de
.
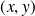On appelle mesure de l'angle
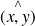tout réel
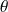tel que la matrice de la rotation
soit
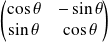dans une base orthonormale directe.
Toutes les mesures d'un angle orienté sont congrues modulo
.
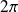L'angle orienté de deux vecteurs non nuls
et
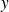est l'angle orienté des vecteurs unitaires associés
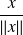et
.
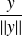Les rotations conservent le sens des angles orientés :
.
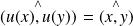Les réflexions changent le sens des angles orientés :
.
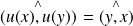Fondamental :
Caractéristiques d'un endomorphisme orthogonal en dimension 2
Si
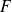est l'ensemble des vecteurs invariants de l'endomorphisme
:
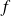Si
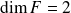, alors
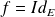.Si
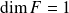, alors
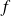est la réflexion par rapport à la droite
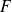. Si la matrice de
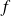est
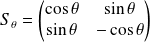, un vecteur directeur de l'axe
de la réflexion est :
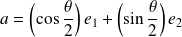.L'axe de la réflexion est la droite vectorielle d'équation :
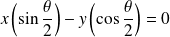.Si
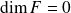, alors
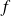est une rotation d'angle non nul de mesure
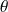si la matrice de
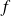est
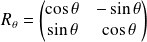.Alors, pour tout vecteur unitaire
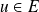, on a :
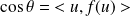et
.
