Exercice 9
Commencez par chercher à résoudre l'exercice par vous-même.
Si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
Question
Montrer que, si
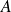 est une matrice symétrique réelle :
est une matrice symétrique réelle :
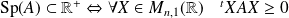 .
.
Démontrez successivement les deux implications.
Utilisez la diagonalisation de la matrice et montrez que, pour toute valeur propre
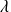 , il existe
, il existe
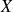 telle que
telle que
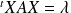 .
.
Si la matrice
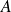 est symétrique réelle, elle est diagonalisable :
est symétrique réelle, elle est diagonalisable :
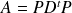 où
où
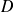 est diagonale.
est diagonale.
Donc :
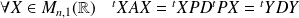 en posant :
en posant :
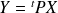 .
.
Soient
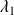 , ...,
, ...,
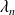 les valeurs propres de
les valeurs propres de
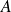 comptées avec leur ordre de multiplicité.
comptées avec leur ordre de multiplicité.
Donc :
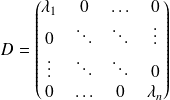 . Et si
. Et si
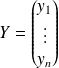 , alors :
, alors :
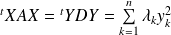 .
.
Montrons successivement les deux implications :
Supposons que :
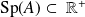 . Donc :
. Donc :
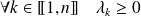 .
.Donc :
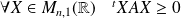 car
car
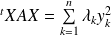 .
.
Réciproquement, supposons que
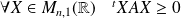 .
.La matrice
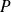 est inversible et
est inversible et
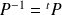 . Donc :
. Donc :
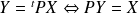 .
.Pour tout
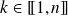 , on note
, on note
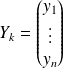 avec
avec
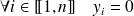 si
si
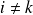 et
et
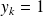 .
.Et, pour tout
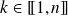 , on note
, on note
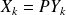 . Donc :
. Donc :
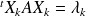 .
.Or, d'après l'hypothèse :
 , donc
, donc
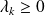 .
.Donc :
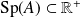 .
.
Conclusion : Si
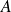 est symétrique, alors
est symétrique, alors
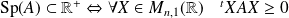 .
.
Question
En déduire que, pour toute matrice réelle
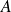 , la matrice
, la matrice
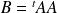 est diagonalisable et que ses valeurs propres sont positives.
est diagonalisable et que ses valeurs propres sont positives.
Utilisez la question précédente.
La matrice
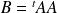 est réelle et :
est réelle et :
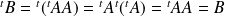 .
.
Donc
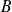 est une matrice symétrique réelle. Donc
est une matrice symétrique réelle. Donc
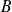 est diagonalisable.
est diagonalisable.
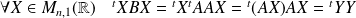 en posant
en posant
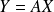 .
.
Or si
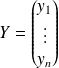 , alors
, alors
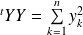 . Donc :
. Donc :
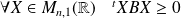 .
.
Donc d'après la première question :
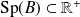 .
.
Conclusion : La matrice
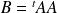 est diagonalisable et ses valeurs propres sont positives.
est diagonalisable et ses valeurs propres sont positives.





