Endomorphismes autoadjoints
Dans ce qui suit,
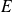désigne un espace vectoriel euclidien.
Définition :
Un endomorphisme
est autoadjoint (ou symétrique) si
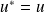, donc si :
.
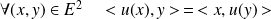Notation : L'ensemble des endomorphismes autoadjoints de
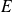est noté
.
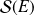Exemple :
Les projections orthogonales et les symétries orthogonales sont des endomorphismes autoadjoints.
Plus précisément, un projecteur
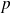est auto-adjoint si et seulement si
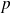est une projection orthogonale.
Fondamental :
Propriétés :
Si
est auto-adjoint, alors :
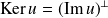et
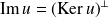.Un endomorphisme
est auto-adjoint si et seulement si sa matrice dans une base orthonormale est symétrique.Théorème spectral : Tout endomorphisme auto-adjoint est diagonalisable dans une base orthonormale et ses valeurs propres sont réelles.
Fondamental :
Conséquences pour les matrices :
Toute matrice symétrique réelle est diagonalisable dans
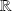.Une matrice réelle carrée
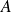est symétrique si et seulement si il existe une matrice
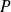telle que la matrice
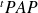soit diagonale.
