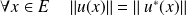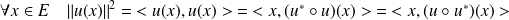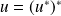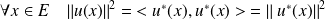Exercice 6
Commencez par chercher à résoudre l'exercice par vous-même.
Si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
Soit
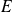 un espace vectoriel euclidien.
un espace vectoriel euclidien.
Soit
 un endomorphisme de
un endomorphisme de
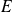 tel que
tel que
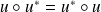 (endomorphisme normal).
(endomorphisme normal).
Question
Question
Démontrer que
 et
et
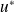 ont les mêmes valeurs propres et les mêmes sous-espaces propres.
ont les mêmes valeurs propres et les mêmes sous-espaces propres.
Calculez
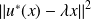 lorsque
lorsque
 est vecteur propre de
est vecteur propre de
 associé à la valeur propre
associé à la valeur propre
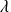 .
.
Soit
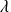 une valeur propre de
une valeur propre de
 et
et
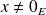 un vecteur propre associé :
un vecteur propre associé :
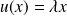 .
.
Donc :
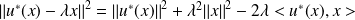 .
.
Donc :
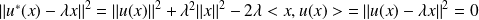 .
.
Donc :
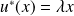 . Donc
. Donc
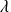 est valeur propre de
est valeur propre de
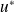 et
et
 est un vecteur propre associé à
est un vecteur propre associé à
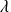 .
.
Notons
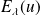 et
et
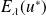 les sous-espaces propres associés.
les sous-espaces propres associés.
Donc :
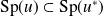 . Et si
. Et si
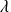 est valeur propre de
est valeur propre de
 , alors :
, alors :
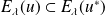 .
.
On applique le même raisonnement à
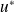 car
car
 et
et
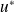 jouent des rôles symétriques.
jouent des rôles symétriques.
Donc :
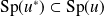 . Et si
. Et si
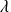 est valeur propre de
est valeur propre de
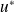 , alors :
, alors :
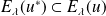 .
.
Donc
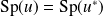 et si
et si
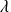 est valeur propre de
est valeur propre de
 , alors :
, alors :
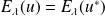 .
.
Conclusion : Les endomorphismes
 et
et
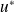 ont les mêmes valeurs propres et les mêmes sous-espaces propres.
ont les mêmes valeurs propres et les mêmes sous-espaces propres.
Question
Démontrer que deux sous-espaces propres associés à des valeurs propres distinctes sont orthogonaux.
Calculez
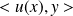 lorsque
lorsque
 et
et
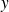 sont dans deux sous-espaces propres distincts.
sont dans deux sous-espaces propres distincts.
Soient deux valeurs propres distinctes
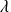 et
et
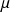 de
de
 (et de
(et de
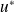 ), et
), et
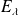 et
et
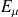 les sous-espaces propres associés.
les sous-espaces propres associés.
Soient
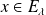 et
et
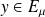 . Donc :
. Donc :
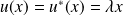 et
et
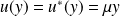 .
.
Donc :
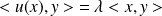 . Or :
. Or :
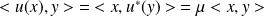 .
.
Donc :
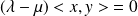 . Or :
. Or :
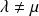 . Donc :
. Donc :
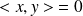 .
.
Donc :
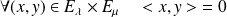 .
.
Conclusion : Deux sous-espaces propres associés à des valeurs propres distinctes sont orthogonaux.