Adjoint d'un endomorphisme
Dans ce qui suit,
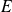désigne un espace vectoriel euclidien.
Définition :
Si
est un endomorphisme de
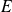, son adjoint est l'endomorphisme
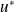tel que :
.
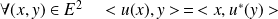En effet, il existe un unique endomorphisme de
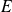qui vérifie cette propriété.
Exemple :
Si
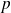est une projection orthogonale :
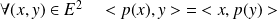. Donc :
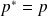.De même, si
est une symétrie orthogonale :
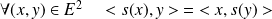. Donc :
.
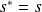Fondamental :
Propriétés :
Si
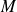est la matrice de
dans une base orthonormale, la matrice de
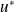est
.
. 
.
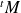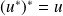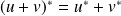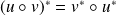.Si
est bijectif,
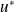est bijectif 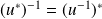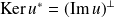et
.
et
.
. 
. 
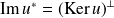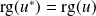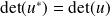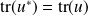.Les endomorphismes
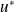et
ont même polynôme caractéristique et mêmes valeurs propres :
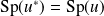.Un sous-espace vectoriel
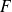est stable par
si et seulement si son orthogonal
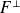est stable par
.
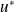Exemple :
Un hyperplan de vecteur normal
est stable par un endomorphisme
si et seulement si
est un vecteur propre de
.
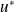Et inversement un vecteur non nul
est vecteur propre d'un endomorphisme
si et seulement si son hyperplan orthogonal est stable par
.
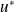