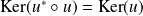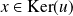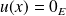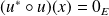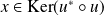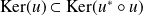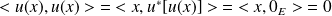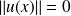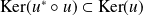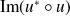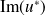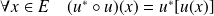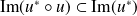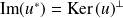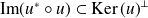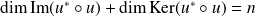Exercice 5
Commencez par chercher à résoudre l'exercice par vous-même.
Si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
Soit
 un endomorphisme d'un espace vectoriel euclidien
un endomorphisme d'un espace vectoriel euclidien
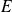 de dimension
de dimension
 .
.
Question
Question
Question
En déduire que :
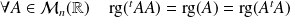 .
.
Indice
Le rang d'une matrice est la dimension de l'image de l'endomorphisme associé.
Solution
Dans
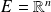 muni du produit scalaire
muni du produit scalaire
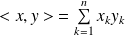 , la base canonique est orthonormale.
, la base canonique est orthonormale.
Soit
 l'endomorphisme de matrice
l'endomorphisme de matrice
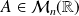 dans cette base.
dans cette base.
Alors
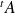 est la matrice de
est la matrice de
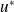 ,
,
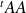 est celle de
est celle de
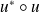 et
et
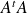 celle de
celle de
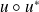 dans cette base.
dans cette base.
Or :
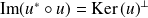 , donc :
, donc :
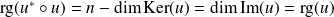 .
.
Le même raisonnement appliqué à
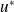 donne :
donne :
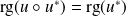 .
.
Or :
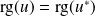 . Donc :
. Donc :
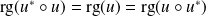 .
.
Conclusion :
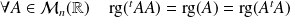 .
.