Exercice 2
Commencez par chercher à résoudre l'exercice par vous-même.
Si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
Soit
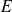un espace vectoriel euclidien.
Question
Montrer qu'une projection
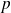est orthogonale si et seulement si :
.
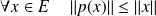Démontrez successivement les deux implications.
Remarquez que :
.
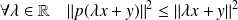On sait déjà que si
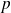est une projection orthogonale, alors :
.
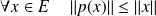En effet, c'est une conséquence du théorème de Pythagore car
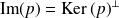, et donc :
.
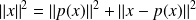Il reste à montrer la réciproque.
Supposons que
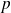est une projection et que :
.
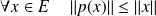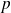est une projection, donc :
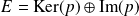. Montrons que :
.
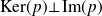Soit
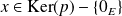et
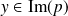. On a :
.
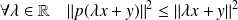Or
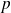est linéaire,
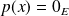et
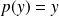. Donc :
.
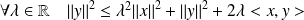Donc :
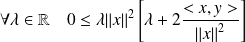puisque
.
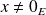Donc, pour
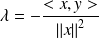, on a :
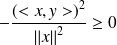, donc :
.
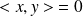Et si
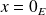, on a évidemment
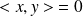pour tout
.
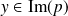Donc :
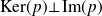. Donc
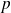est une projection orthogonale.
Conclusion : Une projection
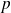est orthogonale si et seulement si :
.
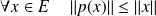Question
Montrer qu'une symétrie
est orthogonale si et seulement si :
.
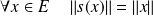Utiliser la projection associée.
On sait déjà que si
est une symétrie orthogonale, alors :
.
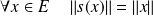En effet
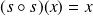, donc
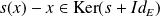et
.
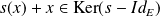Donc :
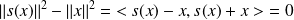car
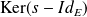et
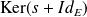sont orthogonaux.
Il reste à montrer la réciproque.
Supposons que
est une symétrie et que :
.
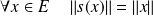Si
est la symétrie par rapport à un sous-espace
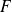parallèlement à un sous-espace
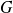, la projection
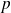sur
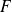parallèlement à
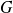est
.
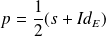Donc :
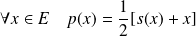, donc :
.
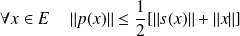Or :
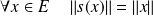, donc :
.
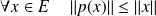Donc, d'après la question précédente,
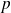est une projection orthogonale :
.
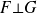Donc
est une symétrie orthogonale.
Conclusion : Une symétrie
est orthogonale si et seulement si :
.
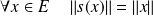