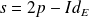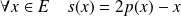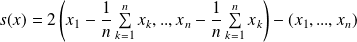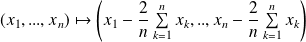Exercice 1
Commencez par chercher à résoudre l'exercice par vous-même.
Si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
On munit l'espace vectoriel
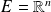du produit scalaire
.
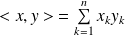Soit le sous-espace vectoriel
.
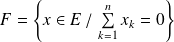Question
Déterminer la projection orthogonale sur
.
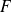Déterminez le supplémentaire orthogonal de
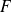et caractérisez la projection.
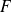est un hyperplan car c'est le noyau de la forme linéaire :
.
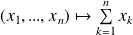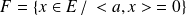où
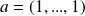. Donc
.
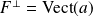Soit
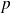la projection orthogonale sur
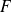. Donc :
.
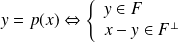Donc
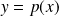si et seulement si :
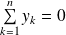et
.
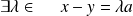Donc
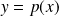si et seulement si :
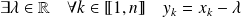et
.
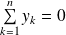On obtient donc :
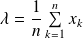. Donc :
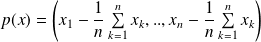
Conclusion : La projection orthogonale sur
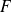est l'application
.
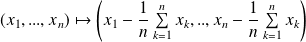