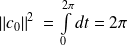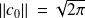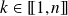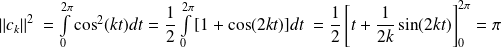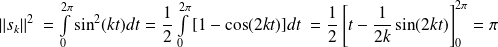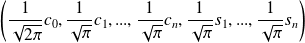Exo 11
Commencez par chercher à résoudre l'exercice par vous-même.
Si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
Soit
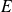 l'espace vectoriel des fonctions continues sur
l'espace vectoriel des fonctions continues sur
 à valeurs dans
à valeurs dans
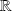 .
.
On munit l'espace vectoriel
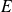 du produit scalaire :
du produit scalaire :
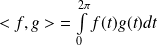 .
.
Soit un entier
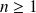 .
.
On définit les fonctions
 et
et
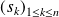 par :
par :
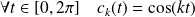 et
et
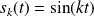 .
.
Et pour toute fonction
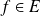 et tout entier
et tout entier
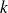 , on pose :
, on pose :
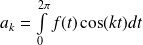 et
et
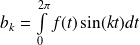 .
.
Question
Montrer que la famille
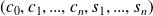 est une famille orthogonale de
est une famille orthogonale de
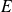 .
.
Montrez que tous les produits scalaires de deux vecteurs de la famille sont nuls.
Utilisez la linéarisation[1] pour calculer les intégrales.
Etudions tous les produits scalaires de deux vecteurs de la famille.
Pour tous
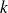 et
et
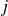 distincts dans
distincts dans
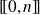 :
:
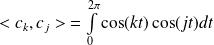 .
.Donc, en linéarisant :
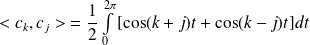 .
.Donc :
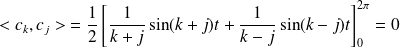 .
.
Pour tous
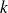 et
et
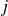 distincts dans
distincts dans
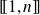 :
:
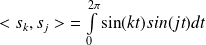 .
.Donc, en linéarisant :
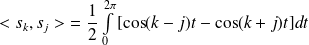 .
.Donc :
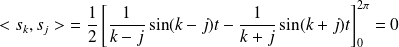 .
.
Pour tous
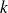 et
et
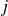 distincts dans
distincts dans
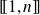 :
:
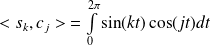 .
.Donc, en linéarisant :
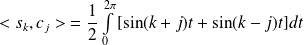 .
.Donc :
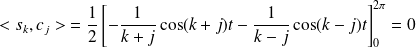 .
.
Pour tout
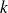 dans
dans
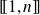 :
:
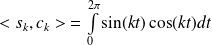 .
.Donc, en linéarisant :
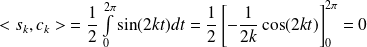 .
.
Pour tout
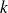 dans
dans
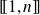 :
:
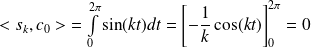 .
.
Conclusion : La famille
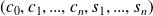 est une famille orthogonale de
est une famille orthogonale de
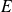 .
.
Question
Question
En déduire que, pour toute fonction
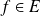 , la série
, la série
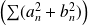 est convergente et que :
est convergente et que :
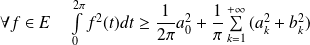 .
.
Utilisez le résultat de l'exercice précédent.
On utilise le résultat de l'exercice précédent pour cette famille orthonormale.
Donc :
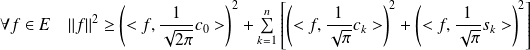 .
.
Donc :
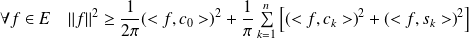 .
.
Or :
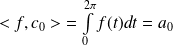 .
.
Et :
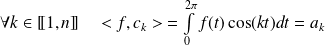 et
et
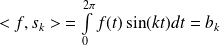 .
.
Donc, pour tout entier
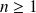 , on a :
, on a :
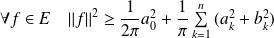 .
.
Soit
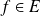 et :
et :
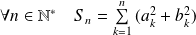 . Donc :
. Donc :
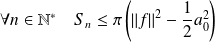 .
.
Donc la série à termes positifs
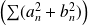 est convergente puisque ses sommes partielles sont majorées.
est convergente puisque ses sommes partielles sont majorées.
Et :
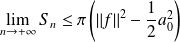 . Donc :
. Donc :
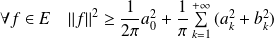 .
.
Conclusion : Pour toute fonction
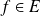 , la série
, la série
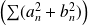 est convergente et :
est convergente et :
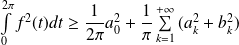 .
.
Exemple : Exemple
On suppose que :
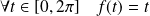 .
.
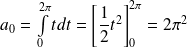 .
.
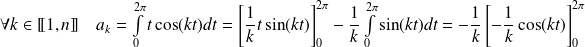 .
.Donc :
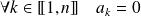 .
.
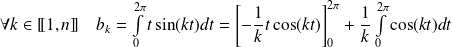 .
.Donc :
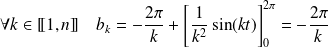 .
.
Donc :
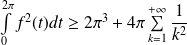 . Or :
. Or :
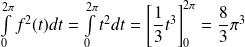 .
.
Donc l'inégalité donne :
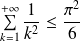 .
.
En réalité, on a une égalité, mais ce qui précède ne donne que l'inégalité.