Exo 10
Commencez par chercher à résoudre l'exercice par vous-même.
Si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
Soit
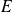un espace vectoriel muni d'un produit scalaire.
Soit
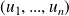une famille orthonormale de
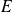et soit
.
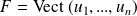Question
Démontrer que :
.
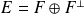Pour tout
de
, dé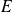terminez
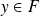tel que
soit orthogonal à tous les vecteurs de
.
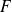Remarque :
Remarquons que
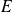n'est pas nécessairement de dimension finie, donc que
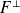n'est pas toujours un supplémentaire de
.
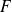Soit
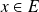et
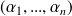des réels. Soit
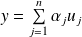et
.
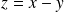Par construction :
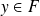. Et
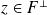si et seulement si :
.
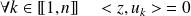Or :
.
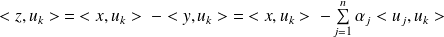Or la famille
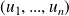est orthonormale. Donc :
.
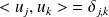Donc :
.
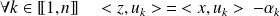Donc
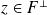si et seulement si :
.
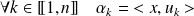On en déduit que :
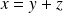avec
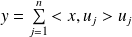, donc
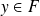et
.
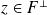Donc :
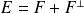. De plus :
.
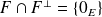Conclusion :
.
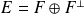Question
En déduire que :
.
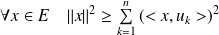Utilisez la décomposition sur
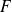et
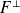, et le théorème de Pythagore.
D'après ce qui précède :
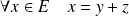avec
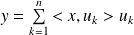et
.
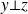Donc d'après le théorème de Pythagore :
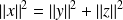, donc :
.
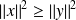Or la famille
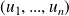est orthonormale, donc :
.
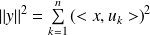Conclusion :
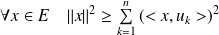(Inégalité de Bessel).
On a une égalité si et seulement si
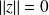, donc si
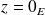, donc si
.
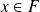