Exo 8
Commencez par chercher à résoudre l'exercice par vous-même.
Si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
Soit
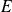 un espace euclidien et
un espace euclidien et
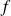 un endomorphisme de
un endomorphisme de
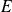 tel que :
tel que :
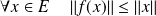 .
.
Question
Montrer que
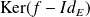 et
et
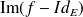 sont des supplémentaires orthogonaux.
sont des supplémentaires orthogonaux.
Démontrez que tout élément de
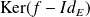 est orthogonal à tout élément de
est orthogonal à tout élément de
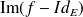 .
.
Remarquez que pour tous les éléments
 et
et
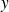 de
de
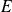 et pour tout réel
et pour tout réel
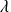 :
:
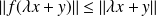 .
.
Soit
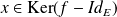 et
et
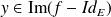 . Donc :
. Donc :
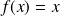 et :
et :
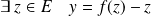 .
.
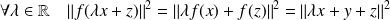 .
.
Donc :
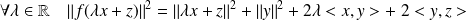 .
.
Or :
 . Donc :
. Donc :
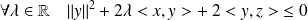 .
.
Si
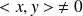 , ce polynôme en
, ce polynôme en
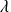 est de degré
est de degré
 , donc il admet une racine et change de signe.
, donc il admet une racine et change de signe.
Or il garde un signe constant. Donc :
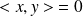 pour tous
pour tous
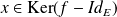 et
et
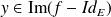 .
.
Donc
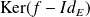 et
et
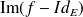 sont des sous-espaces orthogonaux.
sont des sous-espaces orthogonaux.
Et d'après le théorème du rang :
 .
.
Conclusion :
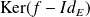 et
et
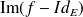 sont des supplémentaires orthogonaux.
sont des supplémentaires orthogonaux.
Question
Démontrer que la suite définie par :
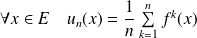 converge vers le projeté de
converge vers le projeté de
 sur
sur
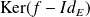 parallèlement à
parallèlement à
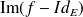 .
.
Décomposez
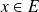 sur
sur
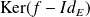 et
et
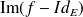 et démontrez que
et démontrez que
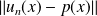 tend vers
tend vers
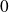 .
.
Soit
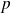 la projection (orthogonale) sur
la projection (orthogonale) sur
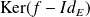 parallèlement à
parallèlement à
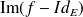 .
.
Soit
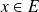 . Donc :
. Donc :
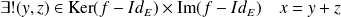 . Et :
. Et :
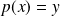 .
.
Or :
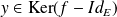 , donc
, donc
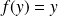 . Et
. Et
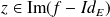 , donc
, donc
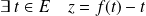 .
.
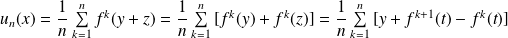 .
.
Donc :
 . Or
. Or
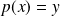 .
.
Donc :
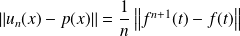 . Donc :
. Donc :
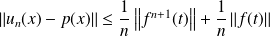 .
.
Or :
 . Donc par une récurrence évidente :
. Donc par une récurrence évidente :
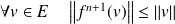 .
.
Donc :
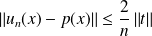 . Donc :
. Donc :
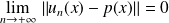 . Donc :
. Donc :
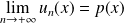 .
.
Conclusion : Pour tout
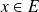 , la suite
, la suite
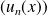 converge vers le projeté orthogonal de
converge vers le projeté orthogonal de
 sur
sur
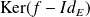 .
.





