Exo 7
Commencez par chercher à résoudre l'exercice par vous-même.
Si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
Soit
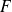un sous-espace vectoriel d'un espace vectoriel
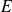muni d'un produit scalaire.
Question
Soit
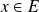. Montrer que s'il existe
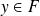tel que
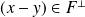, alors :
.
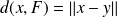Démontrez que :
.
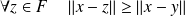Utilisez le théorème de Pythagore.
Supposons qu'il existe
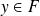tel que
.
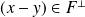Par définition :
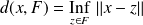. Donc :
.
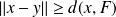Or :
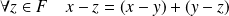, et
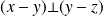car
.
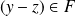Donc :
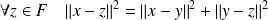, donc :
.
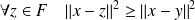Donc :
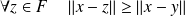. Donc :
.
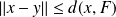Conclusion : S'il existe
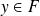tel que
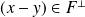, alors :
.
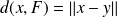Remarque :
Si
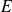est de dimension finie,
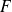et
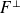sont supplémentaires, donc
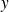existe et c'est le projeté de
sur
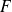parallèlement à
.
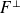Question
En déduire le calcul de :
.
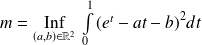Remarquez que le problème revient à déterminer la distance de la fonction exponentielle à un sous-espace vectoriel de l'espace vectoriel
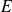des fonctions continues sur
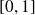muni du produit scalaire
.
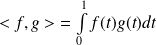Soit
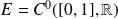l'espace vectoriel des fonctions continues sur
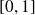muni du produit scalaire :
.
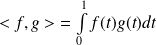Donc
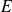n'est pas de dimension finie.
Soit
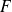l'ensemble des fonctions
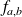définies par :
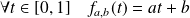où
et
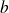sont des réels.
Soit
la fonction définie par :
.
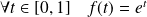Donc :
.
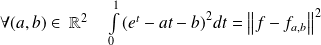Le problème revient donc à déterminer
.
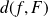Etant donnée la première question, on cherche s'il existe
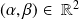tel que
.
Une fonction
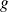appartient à
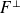si et seulement si elle est orthogonale à toute fonction de
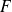, donc si elle est orthogonale à
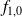et à
, donc si :
.
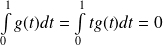On cherche donc s'il existe
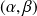tel que
.
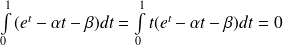Or :
.
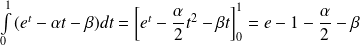Et :
.
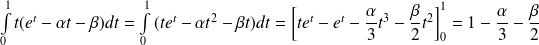On obtient donc le système :
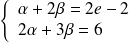. Donc :
.
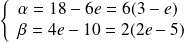Donc il existe
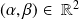tel que
. Donc :
.
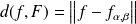Donc :
.
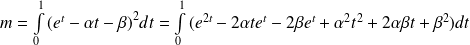Donc :
.
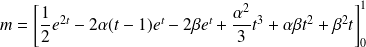Donc :
.
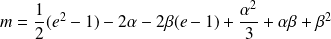Donc :
.
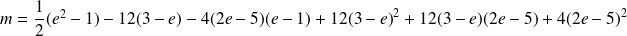Conclusion :
.
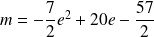