Orthogonalité
Dans ce qui suit,
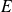désigne un espace vectoriel euclidien (donc de dimension finie).
Définition :
Deux vecteurs
et
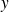de
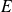sont orthogonaux si :
.
Théorème de Pythagore :
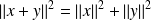si et seulement si
et
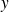sont orthogonaux.
Définition :
Deux parties
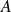et
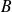sont orthogonales si :
.
L'orthogonal d'une partie
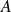non vide est le sous-espace vectoriel :
.
Exemple :
L'orthogonal d'un vecteur non nul de
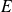est un hyperplan de
.
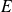Réciproquement, tout hyperplan de
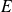est l'orthogonal d'au moins un vecteur non nul.
Si
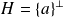, on dira que
est un vecteur normal à
.
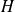En effet, pour toute forme linéaire
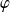sur un espace euclidien
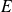, il existe un unique
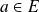tel que :
.
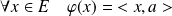Définition :
Si
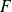est un sous-espace vectoriel, alors :
.
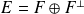Le sous-espace vectoriel
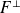est appelé supplémentaire orthogonal de
.
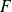C'est le seul sous-espace vectoriel orthogonal à
.
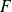Fondamental :
Propriétés :
si
.
.
.
.
.
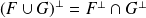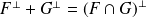Remarque :
Si l'espace vectoriel
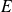n'est pas de dimension finie,
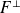n'est pas toujours un supplémentaire de
.
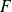Par exemple, dans
muni du produit scalaire
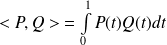, l'orthogonal du sous espace vectoriel
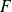des polynômes
tels que
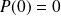est :
.
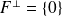En effet, tout polynôme
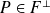doit être orthogonal au polynôme
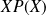qui s'annule en
.
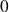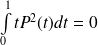Donc :
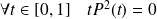, donc :
, donc :
, donc :
.
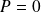