Exo 12
Commencez par chercher à résoudre l'exercice par vous-même.
Si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
Soit
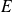un
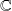- espace vectoriel de dimension
et
un endomorphisme de
.
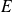Soit
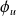l'application qui à tout endomorphisme
de
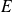associe
.
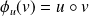Question
Démontrer que
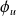est diagonalisable si et seulement si
est diagonalisable.
Démontrez successivement les deux implications en construisant des bases de vecteurs propres.
On démontre successivement les deux implications :
On suppose que
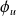est diagonalisable. Or, si
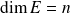, alors
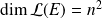.Donc, dans
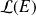, il existe une base
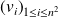de vecteurs propres de
:
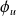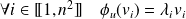. Donc :
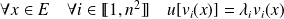.Soit
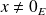. Pour tout
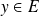, il existe au moins un endomorphisme
tel que
.
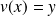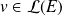, donc il existe des complexes
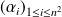tels que
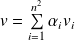.Donc, pour tout
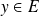, il existe
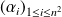tels que
.Donc la famille
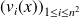est une famille génératrice de
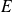. Donc on peut en extraire une base de
:
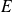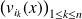.Et :
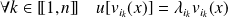, donc
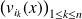est une base de vecteurs propres de
. Donc
est diagonalisable.
On suppose que
est diagonalisable. Donc il existe une base
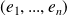de vecteurs propres de
:
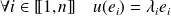.Pour tous
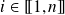et
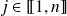, on définit l'endomorphisme
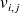tel que
si
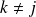et
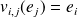.Ces
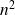endomorphismes ont pour matrices, dans la base
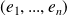, la base canonique de
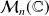. Donc ils sont indépendants, et donc ils forment une base de
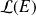.Donc :
si
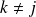et
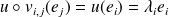.Donc :
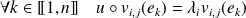. Donc :
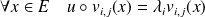.Donc :
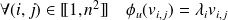. Donc la famille
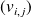est une base de vecteurs propres de
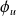. Donc
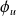est diagonalisable.
Conclusion :
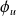est diagonalisable si et seulement si
est diagonalisable.
