Exo 11
Commencez par chercher à résoudre l'exercice par vous-même.
Si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
Soient
et
deux matrices non nulles de
telles que
.
Question
Démontrer que
et
sont semblables. Est-ce encore le cas dans
?
Démontrez que les matrices
et
sont semblables à une même matrice triangulaire.
Soit
l'endomorphisme de
de matrice
dans la base canonique.
, donc
, donc
, donc
.
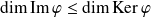Or, d'après le théorème du rang :
. Donc
.
Donc
, et
, donc
et
.
Soit
, donc
, donc
est une base de
.
Or
, donc on peut la compléter en une base
de
.
La famille
est libre, donc c'est une base de
, donc
est semblable à la matrice
.
Le raisonnement est identique pour la matrice
, qui est donc aussi semblable à
.
Conclusion : Dans
, les matrices
et
sont semblables.
Par contre, dans
, le même raisonnement conduit à
ou
.
Or deux matrices semblables ont le même rang.
Conclusion : Dans
, les matrices
et
ne sont pas toujours semblables.
Par exemple, les matrices
et
ne sont pas semblables.
