Exo 10
Commencez par chercher à résoudre l'exercice par vous-même.
Si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
Soient
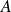 et
et
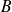 deux matrices de
deux matrices de
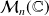 .
.
Question
Démontrer que si
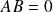 , les matrices
, les matrices
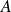 et
et
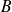 ont un vecteur propre commun.
ont un vecteur propre commun.
Utilisez la restriction de
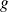 (endomorphisme de matrice
(endomorphisme de matrice
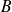 ) à
) à
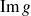 .
.
Soient
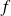 et
et
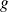 les endomorphismes de
les endomorphismes de
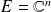 de matrices
de matrices
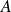 et
et
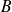 dans la base canonique.
dans la base canonique.
On suppose que
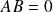 , donc :
, donc :
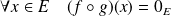 .
.
Si
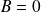 ,
,
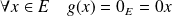 , donc tout vecteur non nul de
, donc tout vecteur non nul de
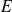 est vecteur propre de
est vecteur propre de
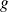 , donc tout vecteur propre de
, donc tout vecteur propre de
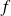 est vecteur propre de
est vecteur propre de
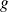 .
.
Si
 , alors
, alors
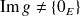 et
et
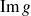 est stable par
est stable par
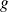 , donc
, donc
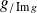 est un endomorphisme de
est un endomorphisme de
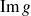 qui possède au moins un vecteur propre
qui possède au moins un vecteur propre
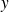 .
.
Donc
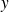 est aussi vecteur propre de
est aussi vecteur propre de
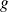 , et
, et
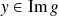 , donc
, donc
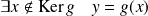 .
.
Or
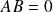 , donc :
, donc :
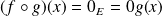 , donc
, donc
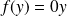 et
et
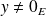 .
.
Donc,
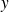 est aussi vecteur propre de
est aussi vecteur propre de
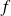 . Donc
. Donc
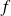 et
et
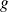 ont un vecteur propre commun.
ont un vecteur propre commun.
Conclusion : Si
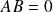 , les matrices
, les matrices
 et
et
 ont un vecteur propre commun.
ont un vecteur propre commun.
Question
Démontrer que si
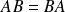 , les matrices
, les matrices
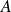 et
et
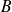 ont un vecteur propre commun.
ont un vecteur propre commun.
Utilisez la restriction de
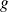 (endomorphisme de matrice
(endomorphisme de matrice
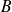 ) à un sous-espace propre de
) à un sous-espace propre de
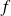 (endomorphisme de matrice
(endomorphisme de matrice
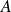 ).
).
On suppose que
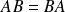 , donc :
, donc :
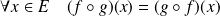 .
.
L'endomorphisme
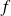 admet au moins une valeur propre
admet au moins une valeur propre
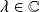 . Soit
. Soit
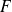 le sous-espace propre associé :
le sous-espace propre associé :
 .
.
Donc :
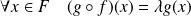 , donc
, donc
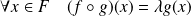 .
.
Donc :
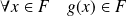 . Donc
. Donc
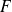 est stable par
est stable par
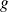 et
et
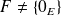 .
.
Donc
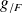 est un endomorphisme de
est un endomorphisme de
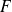 qui possède au moins un vecteur propre
qui possède au moins un vecteur propre
 .
.
Donc
 est vecteur propre de
est vecteur propre de
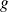 (donc non nul) et appartient à
(donc non nul) et appartient à
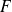 .
.
Donc
 est aussi vecteur propre de
est aussi vecteur propre de
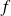 . Donc
. Donc
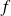 et
et
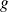 ont un vecteur propre commun.
ont un vecteur propre commun.
Conclusion : Si
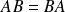 , les matrices
, les matrices
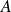 et
et
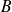 ont un vecteur propre commun.
ont un vecteur propre commun.





