Exo 3
Commencez par chercher à résoudre l'exercice par vous-même.
Si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
Soit
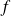un endomorphisme d'un espace vectoriel
.
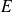Question
Montrer que si la famille
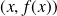est liée pour tout
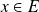, alors
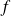est une homothétie.
Exprimez que la famille
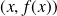est liée par
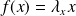, puis démontrez que
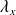ne dépend pas de
.
La famille
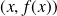est liée pour tout
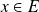. Donc
.
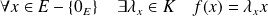Il s'agit de montrer que
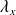ne dépend pas de
.
Soit
un vecteur non nul de
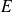. La famille
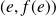est liée, donc il existe un scalaire
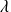tel que
.
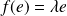Soit
un vecteur quelconque de
.
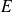Si
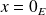, alors
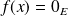, donc
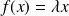.Si
est colinéaire à
et
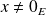, il existe un scalaire
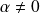tel que
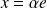. Donc
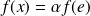, donc
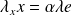, donc
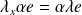, donc
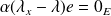. Donc
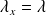.Si
n'est pas colinéaire à
, la famille
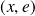est libre. Or
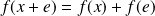, donc
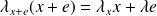. Donc
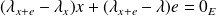. Or la famille
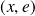est libre. Donc :
.
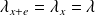Donc dans tous les cas, on a
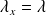, donc
.
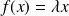Donc :
.
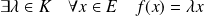Conclusion : L'application
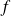est une homothétie.
