Applications linéaires
Définition :
Soient
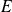et
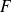deux espaces vectoriels. Une application
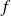de
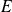dans
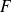est linéaire si :
.
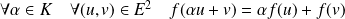Un endomorphisme de
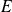est une application linéaire de
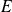dans
.
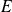Un isomorphisme est une application linéaire bijective de
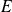dans
.
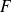Un automorphisme de
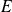est un endomorphisme bijectif de
.
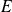Exemple :
L'application qui à tout
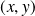de
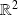associe
est une application linéaire de
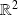dans
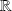.Si
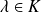, l'homothétie de rapport
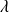qui à tout vecteur
de
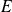associe le vecteur
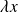est un endomorphisme de
.
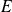Fondamental :
Opérations :
La somme de deux applications linéaires est linéaire.
Le produit par un scalaire d'une application linéaire est linéaire.
La composée de deux applications linéaires est linéaire.
La réciproque d'une application linéaire bijective est linéaire.
Fondamental :
Conséquences :
L'ensemble
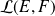des applications linéaires de
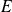dans
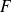est un espace vectoriel.L'ensemble
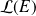des endomorphismes de
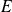est un espace vectoriel.L'ensemble des automorphismes de
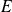muni de la composition des applications est un groupe appelé groupe linéaire de
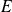et noté
.
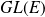