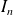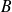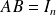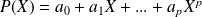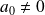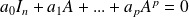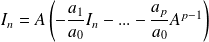Exo 5
Commencez par chercher à résoudre l'exercice par vous-même.
Si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
Soit
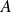une matrice de
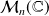et
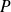un polynôme tel que
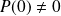et
.
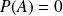Question
On considère la matrice :
.
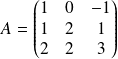Question
Montrer qu'il existe des réels
,
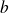et
tels que :
.
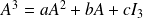En déduire que la matrice
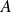est inversible et calculer son inverse.
Indice
Utilisez la méthode précédente.
Solution
.
.
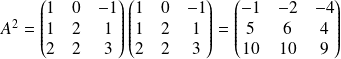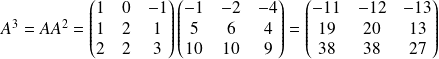Donc :
.
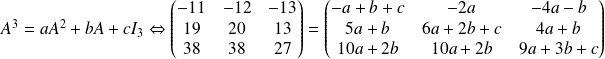Donc
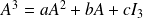si et seulement si
,
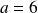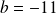et
.
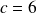Conclusion :
.
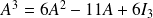Donc, si
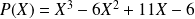, on a
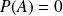et
.
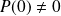Conclusion : La matrice
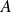est inversible.
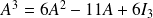, donc :
.
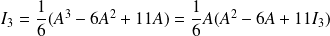Donc la matrice inverse de
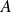est :
.
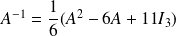Conclusion :
.
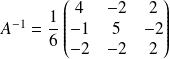