Inversion d'une matrice carrée
Définition :
Une matrice carrée
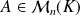est inversible s'il existe une matrice
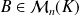telle que
.
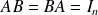Si elle existe, la matrice
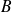est unique et notée
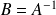. C'est la matrice inverse de la matrice
.
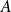Il existe des matrices qui ne sont pas inversibles.
Par exemple, si
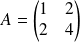, il n'existe pas de matrice
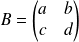telle que
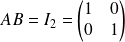car :
.
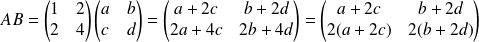Fondamental :
Propriétés :
Si
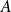est inversible,
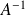est inversible et :
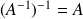. Si
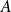et
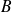sont inversibles,
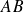est inversible et :
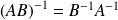. Si
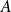est inversible,
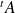est inversible et :
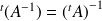.Une matrice triangulaire (ou diagonale) est inversible si et seulement si elle n'a pas de zéros sur la diagonale.
Une matrice
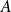est inversible si et seulement si
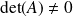. Alors
.
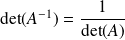Méthode :
On appelle comatrice de
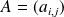, notée
, la matrice des cofacteurs
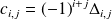où
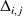est le mineur de
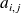(déterminant obtenu en supprimant la ligne
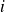et la colonne
).
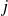Calcul de l'inverse d'une matrice carrée
Si la matrice
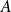est inversible :
.
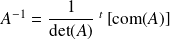Exemple :
Soit
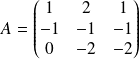. Donc :
.
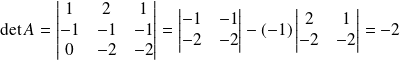La comatrice de
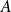est :
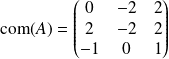. Donc :
.
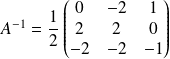Remarque :
Les exercices suivants permettront de voir quelques autres méthodes pour calculer l'inverse d'une matrice carrée :
Utilisation d'un polynôme.
Inversion d'un système.
