Exo 7
Commencez par chercher à résoudre l'exercice par vous-même.
Si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
Question
Démontrer que deux polynômes
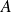et
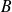sont premiers entre eux si et seulement si les polynômes
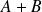et
sont premiers entre eux.
Utilisez le théorème de Bezout.
On démontre successivement les deux implications.
On suppose que
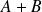et
sont premiers entre eux.Donc il existe
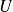et
tels que :
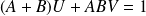, donc
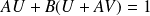.Donc, d'après le théorème de Bezout,
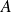et
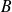sont premiers entre eux.
On suppose que
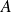et
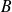sont premiers entre eux.Donc il existe
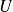et
tels que :
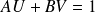.Donc :
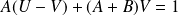, donc :
.Et :
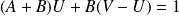, donc :
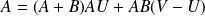.Donc :
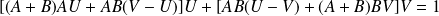.Donc :
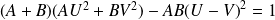.Donc, d'après le théorème de Bezout,
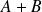et
sont premiers entre eux.
Conclusion :
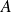et
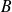sont premiers entre eux si et seulement si
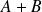et
sont premiers entre eux.
