Division euclidienne
Fondamental :
Division euclidienne :
Si
 et
et
 sont deux polynômes et si
sont deux polynômes et si
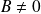 , il existe un unique couple
, il existe un unique couple
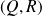 de polynômes tels que :
de polynômes tels que :
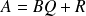 avec
avec
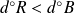 .
.
Si
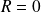 , on dira que
, on dira que
 est divisible par
est divisible par
 , que
, que
 divise
divise
 , que
, que
 est un diviseur de
est un diviseur de
 et que
et que
 est multiple de
est multiple de
 .
.
Fondamental :
Tout idéal de l'anneau
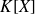 est principal :
est principal :
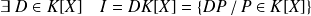 .
.
Si
 et
et
 sont deux polynômes, l'idéal
sont deux polynômes, l'idéal
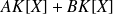 est principal, donc il existe un polynôme
est principal, donc il existe un polynôme
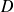 (non unique) tel que :
(non unique) tel que :
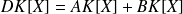 .
.
Ce polynôme
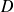 est un diviseur commun à
est un diviseur commun à
 et
et
 , et tout diviseur commun à
, et tout diviseur commun à
 et
et
 divise
divise
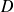 .
.
Définition :
Un polynôme
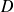 est le PGCD de deux polynômes
est le PGCD de deux polynômes
 et
et
 non tous nuls si :
non tous nuls si :
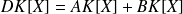 et si
et si
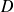 est unitaire. On note :
est unitaire. On note :
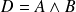 .
.
Si l'un des polynômes est nul, le PGCD est le polynôme unitaire associé à l'autre.
Un polynôme
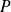 divise
divise
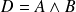 si et seulement si
si et seulement si
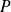 divise
divise
 et
et
 .
.
Fondamental :
Algorithme d'Euclide :
Il s'agit d'une méthode pour déterminer le PGCD de deux polynômes non nuls
 et
et
 . On suppose
. On suppose
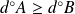 .
.
On définit une suite finie de polynômes
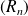 par
par
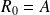 ,
,
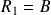 , et, pour tout entier
, et, pour tout entier
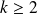 ,
,
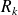 est le reste de la division de
est le reste de la division de
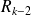 par
par
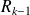 si
si
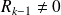 .
.
Le PGCD de
 et
et
 est le polynôme unitaire associé au dernier reste non nul.
est le polynôme unitaire associé au dernier reste non nul.
Exemple :
Exemple : Déterminer le PGCD des polynômes
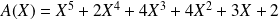 et
et
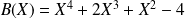 .
.
Si
 et
et
 sont deux polynômes, l'idéal
sont deux polynômes, l'idéal
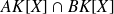 est l'ensemble des multiples communs à
est l'ensemble des multiples communs à
 et
et
 .
.
Définition :
Un polynôme
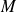 est le PPCM de deux polynômes
est le PPCM de deux polynômes
 et
et
 non nuls si :
non nuls si :
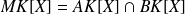 et si
et si
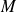 est unitaire. On le note :
est unitaire. On le note :
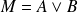 .
.
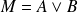 divise un polynôme
divise un polynôme
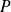 si et seulement si
si et seulement si
 et
et
 divisent
divisent
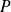 .
.
Si
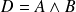 et
et
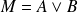 , le polynôme
, le polynôme
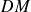 est le polynôme unitaire associé au polynôme
est le polynôme unitaire associé au polynôme
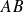 .
.
Fondamental :
Deux polynômes
 et
et
 sont premiers entre eux si :
sont premiers entre eux si :
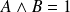 .
.
Propriétés :
Si
 divise
divise
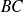 et si
et si
 et
et
 sont premiers entre eux, alors
sont premiers entre eux, alors
 divise
divise
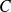 .
.Si
 et
et
 divisent
divisent
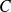 et si
et si
 et
et
 sont premiers entre eux, alors
sont premiers entre eux, alors
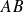 divise
divise
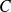 .
.
Théorème de Bezout :
Deux polynômes
 et
et
 sont premiers entre eux si et seulement si il existe un couple
sont premiers entre eux si et seulement si il existe un couple
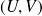 de polynômes tels que :
de polynômes tels que :
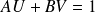 .
.Il y a unicité du couple
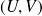 si
si
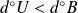 et
et
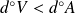 .
.L'algorithme d'Euclide permet de déterminer un couple solution.
Exemple :
Exemple : Montrer que les polynômes
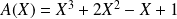 et
et
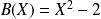 sont premiers entre eux et déterminer des polynômes
sont premiers entre eux et déterminer des polynômes
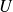 et
et
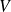 tels que
tels que
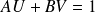 .
.





