Exo 6
Commencez par chercher à résoudre l'exercice par vous-même.
Si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
Soit un entier
 et le polynôme
et le polynôme
 .
.
Question
Déterminer le reste de la division du polynôme
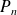 par
par
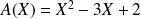 .
.
Déterminez le degré du reste et utilisez les racines du polynôme
 pour calculer les coefficients de ce reste.
pour calculer les coefficients de ce reste.
D'après le théorème de division euclidienne, il existe un unique couple
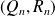 de polynômes tel que :
de polynômes tel que :
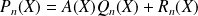 et
et
 .
.
Donc
 . Donc il existe
. Donc il existe
 tel que :
tel que :
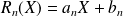 .
.
Or
 . Donc :
. Donc :
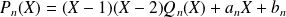 .
.
Donc :
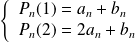 . Donc :
. Donc :
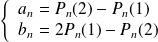 .
.
Or
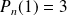 et
et
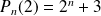 . Et
. Et
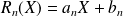 .
.
Conclusion : Le reste de la division de
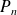 par
par
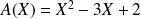 est
est
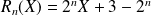 .
.
Question
Déterminer le reste de la division du polynôme
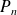 par
par
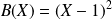 .
.
Ici, le polynôme
 a une racine double, donc la méthode précédente ne donne qu'une équation.
a une racine double, donc la méthode précédente ne donne qu'une équation.
Utilisez le polynôme dérivé de
 pour obtenir une deuxième équation.
pour obtenir une deuxième équation.
D'après le théorème de division euclidienne, il existe un unique couple
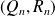 de polynômes tel que :
de polynômes tel que :
 et
et
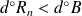 .
.
Donc
 . Donc il existe
. Donc il existe
 tel que :
tel que :
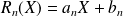 .
.
Donc :
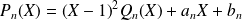 .
.
Et :
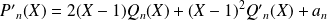 .
.
Donc :
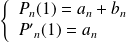 . Donc :
. Donc :
 .
.
Or
 . Donc
. Donc
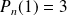 et
et
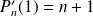 . Et
. Et
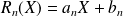 .
.
Conclusion : Le reste de la division de
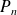 par
par
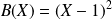 est
est
 .
.
Question
Déterminer le reste de la division du polynôme
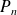 par
par
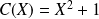 .
.
Ici le polynôme
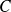 n'a pas de racine réelle, mais a deux racines complexes.
n'a pas de racine réelle, mais a deux racines complexes.
Utilisez la méthode de la première question dans l'ensemble des polynômes complexes, puis montrez que les coefficients sont réels.
D'après le théorème de division euclidienne, il existe un unique couple
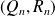 de polynômes tel que :
de polynômes tel que :
 et
et
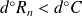 .
.
Donc
 . Donc il existe
. Donc il existe
 tel que :
tel que :
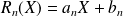 .
.
Donc :
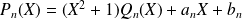 .
.
Or
 . Donc :
. Donc :
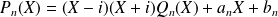 .
.
Donc :
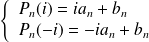 . Donc :
. Donc :
 .
.
Or :
 et
et
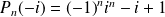 .
.
Donc :
 et
et
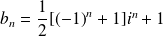 .
.
Or
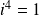 , donc l'expression de
, donc l'expression de
 dépend de la congruence de
dépend de la congruence de
 modulo
modulo
 .
.
Si
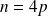 avec
avec
 entier :
entier :
 et
et
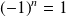 , donc
, donc
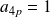 et
et
 .
.
Si
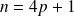 avec
avec
 entier :
entier :
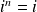 et
et
 , donc
, donc
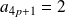 et
et
 .
.
Si
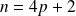 avec
avec
 entier :
entier :
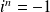 et
et
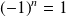 , donc
, donc
 et
et
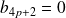 .
.
Si
 avec
avec
 entier :
entier :
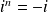 et
et
 , donc
, donc
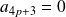 et
et
 .
.
Conclusion : Le reste de la division de
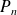 par
par
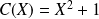 est :
est :
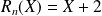 si
si
 .
.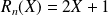 si
si
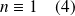 .
.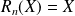 si
si
 .
.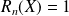 si
si
 .
.





