Exo 3
Commencez par chercher à résoudre l'exercice par vous-même.
Si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
Question
Déterminer les polynômes
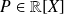qui vérifient :
.
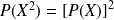Commencez par déterminer son coefficient dominant
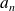, puis étudiez le polynôme
.
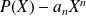Il est évident que le polynôme nul est solution. Cherchons les autres solutions.
Soit
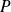un polynôme non nul solution de l'équation. Soit
son degré, et
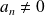son coefficient dominant.
Le polynôme
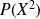a pour degré
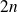et pour coefficient dominant
.
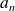Le polynôme
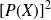a pour degré
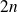et pour coefficient dominant
.
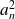Or
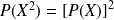. Donc
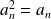. Or
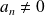, donc
.
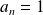Donc
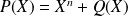où
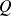est le polynôme nul ou un polynôme de degré
.
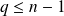Supposons que le polynôme
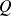ne soit pas le polynôme nul.
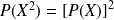. Donc :
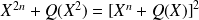. Donc :
.
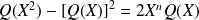Or le polynôme
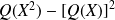est de degré inférieur ou égal à
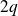et le polynôme
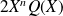est de degré
.
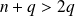On aboutit à une contradiction. Donc l'hypothèse est fausse. Donc
.
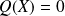Donc toute solution non nulle de l'équation est de la forme
.
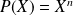Réciproquement, il est évident que tous les polynômes de cette forme sont solutions.
Conclusion : Les solutions sont les polynômes de la forme
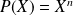avec
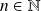ou
.
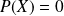Remarque :
Une autre méthode consiste à démontrer que 0 est la seule racine possible du polynôme.
En effet, si
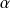est racine de
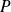, alors
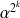est aussi racine de
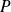pour tout entier
.
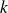Comme un polynôme ne peut pas avoir une infinité de racines, il faut que
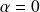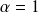ou
ou
.
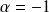Donc le polynôme
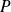est de la forme :
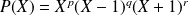. Et l'on démontre que
.
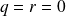