Exo 1
Commencez par chercher à résoudre l'exercice par vous-même.
Si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
Question
Déterminer les polynômes
qui vérifient :
.
Commencez par déterminer le degré de
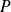, puis déterminez ses coefficients.
Il est évident que le polynôme nul est solution. Cherchons les autres solutions.
Soit
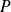un polynôme non nul solution de l'équation.
Si le polynôme
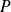est de degré
, alors le polynôme
est de degré
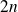et le polynôme
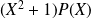est de degré
.
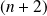Donc il faut que :
, donc
.
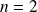Donc il existe des réels
,
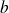et
tels que
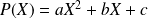avec
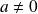. Et :
.
Donc :
.
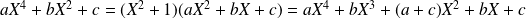Donc :
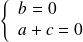. Donc :
.
Réciproquement, si
, alors :
.
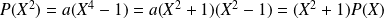Donc le polynôme
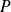est solution de l'équation.
Pour
, on retrouve le polynôme nul.
Conclusion : Les solutions sont les polynômes de la forme
où
.
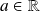