Exo 5
Commencez par chercher à résoudre l'exercice par vous-même.
Si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
On considère l'équation
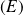 :
:
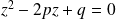 , où
, où
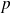 et
et
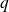 sont deux nombres complexes donnés avec
sont deux nombres complexes donnés avec
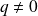 .
.
Question
Montrer que les solutions de
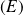 ont même argument si et seulement si
ont même argument si et seulement si
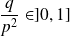 .
.
Démontrez successivement les deux implications.
Dans un sens, exprimez les racines sous forme trigonométrique.
Dans l'autre, calculez le discriminant et les racines.
Remarquons d'abord que les solutions de
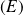 ne sont pas nulles car
ne sont pas nulles car
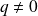 .
.
On suppose que les solutions
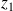 et
et
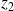 de
de
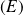 ont même argument
ont même argument
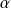 .
.Donc il existe deux réels
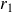 >0 et
>0 et
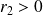 tels que :
tels que :
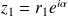 et
et
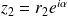 .
.Donc :
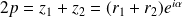 et
et
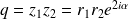 . Donc
. Donc
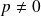 car
car
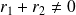 .
.Donc :
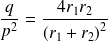 est un réel strictement positif. Et
est un réel strictement positif. Et
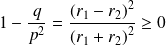 .
.Donc
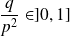 .
.On suppose que
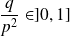 (donc
(donc
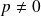 ), donc :
), donc :
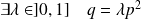 .
.Le discriminant de l'équation est :
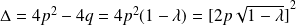 .
.Donc les solutions de
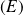 sont
sont
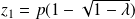 et
et
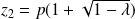 .
.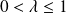 , donc
, donc
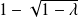 et
et
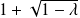 sont des réels strictement positifs.
sont des réels strictement positifs.Donc
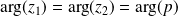 .
.
Conclusion : Les solutions de
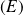 ont même argument si et seulement si
ont même argument si et seulement si
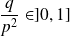 .
.
Question
Montrer que les solutions de
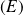 ont même module si et seulement si
ont même module si et seulement si
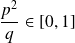 .
.
Démontrez successivement les deux implications.
Dans un sens, exprimez les racines sous forme trigonométrique.
Dans l'autre, calculez le discriminant et les racines.
On suppose que les solutions
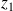 et
et
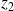 de
de
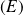 ont même module
ont même module
 .
.Donc il existe deux réels
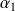 et
et
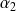 tels que :
tels que :
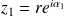 et
et
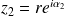 .
.Donc :
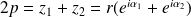 et
et
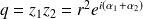 .
.Donc
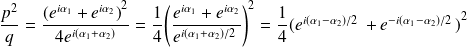 .
.Donc :
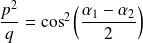 .
. Donc :
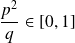 .
.On suppose que
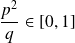 . Donc
. Donc
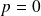 ou
ou
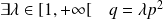 .
.Si
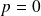 , alors
, alors
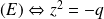 . Donc :
. Donc :
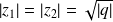 .
.Si
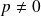 , le discriminant de l'équation est :
, le discriminant de l'équation est :
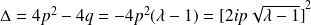 .
.Donc les solutions de
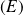 sont
sont
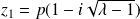 et
et
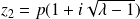 .
.Les complexes
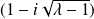 et
et
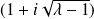 sont conjugués. Donc ils ont le même module
sont conjugués. Donc ils ont le même module
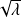 .
. Donc
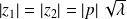 .
.
Conclusion : Les solutions de
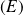 ont même module si et seulement si
ont même module si et seulement si
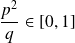 .
.





