Exo 3
Commencez par chercher à résoudre l'exercice par vous-même.
Si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
Soit
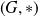 un groupe,
un groupe,
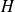 et
et
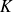 deux sous-groupes de
deux sous-groupes de
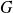 .
.
Question
Démontrer que
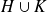 est un sous-groupe de
est un sous-groupe de
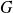 si et seulement si
si et seulement si
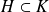 ou
ou
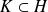 .
.
Si
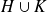 est un sous-groupe de
est un sous-groupe de
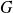 , supposez par exemple que
, supposez par exemple que
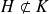 et démontrez que
et démontrez que
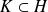 .
.
Supposons que
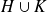 est un sous-groupe de
est un sous-groupe de
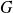 .
.Donc :
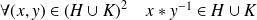 .
.Si
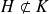 , il existe
, il existe
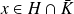 et
et
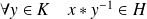 ou
ou
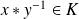 .
.Si
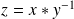 appartenait à
appartenait à
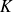 , on aurait
, on aurait
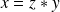 , donc
, donc
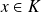 , ce qui est faux.
, ce qui est faux.Donc
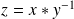 appartient à
appartient à
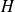 pour tout
pour tout
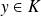 . Or
. Or
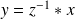 , donc :
, donc :
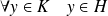 .
.Donc si
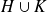 est un sous-groupe de
est un sous-groupe de
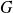 et si
et si
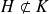 , alors
, alors
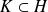 .
.Donc si
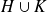 est un sous-groupe de
est un sous-groupe de
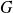 , alors
, alors
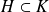 ou
ou
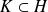 .
.
La réciproque est évidente puisque si
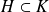 ou
ou
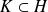 , on a
, on a
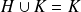 ou
ou
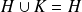 .
.
Conclusion :
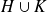 est un sous-groupe de
est un sous-groupe de
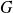 si et seulement si
si et seulement si
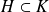 ou
ou
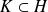 .
.
Question
Soit
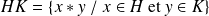 .
.
Démontrer que
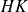 est un sous-groupe de
est un sous-groupe de
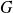 si et seulement si
si et seulement si
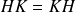 .
.
Démontrez successivement les deux implications.
Remarquez que l'inverse d'un élément de
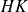 est un élément de
est un élément de
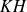 .
.
Supposons que
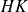 est un sous-groupe de
est un sous-groupe de
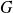 .
.Donc :
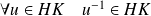 , donc :
, donc :
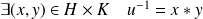 , donc :
, donc :
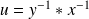 .
.Or
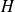 et
et
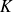 sont des sous groupes de
sont des sous groupes de
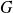 , donc
, donc
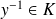 et
et
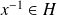 , donc
, donc
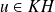 . Donc
. Donc
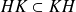 .
.De même :
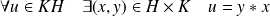 , donc
, donc
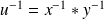 .
.Or
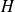 et
et
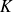 sont des sous groupes, donc
sont des sous groupes, donc
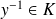 et
et
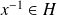 , donc
, donc
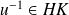 .
.Mais
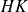 est un sous-groupe de
est un sous-groupe de
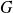 , donc
, donc
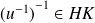 , donc
, donc
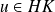 . Donc
. Donc
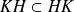 .
.Donc si
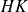 est un sous-groupe de
est un sous-groupe de
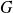 , alors
, alors
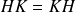 .
.
Réciproquement, supposons que
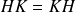 .
.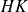 est une partie non vide de
est une partie non vide de
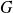 puisqu'elle contient
puisqu'elle contient
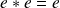 élément neutre de
élément neutre de
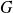 .
.Soit
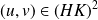 . Donc il existe
. Donc il existe
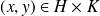 tel que
tel que
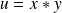 et
et
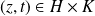 tel que
tel que
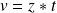 , donc
, donc
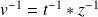 . Donc :
. Donc :
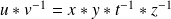 .
.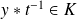 et
et
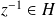 , donc
, donc
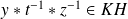 , donc
, donc
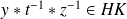 .
.Donc il existe
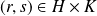 tel que
tel que
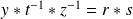 , donc
, donc
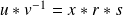 . Or
. Or
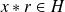 .
.Donc :
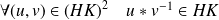 .
.Donc si
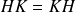 , alors
, alors
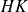 est un sous-groupe de
est un sous-groupe de
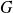 .
.
Conclusion :
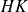 est un sous-groupe de
est un sous-groupe de
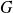 si et seulement si
si et seulement si
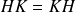 .
.
Remarque :
Dans ce cas,
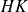 est le sous-groupe engendré par
est le sous-groupe engendré par
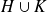 , ce qui explique qu'il faut que
, ce qui explique qu'il faut que
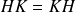 .
.





