Structure de groupe
Définition :
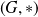est un groupe si la loi
est une loi de composition interne, associative, d'élément neutre
, et si tout élément
a un symétrique
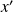dans
.
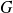Le groupe est commutatif (ou abélien) si la loi
est commutative.
Exemple :
L'ensemble
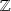des entiers relatifs est un groupe abélien pour l'addition, mais n'est pas un groupe pour la multiplication.L'ensemble
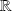des réels est un groupe abélien pour l'addition et l'ensemble
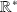est un groupe abélien pour la multiplication.L'ensemble
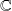des complexes est un groupe abélien pour l'addition et l'ensemble
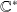est un groupe abélien pour la multiplication.L'ensemble des nombres complexes de module
est un groupe abélien pour la multiplication.
Par contre, l'ensemble
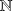des entiers naturels n'est un groupe ni pour l'addition, ni pour la multiplication car ses éléments ne sont pas tous inversibles.
Définition :
Une partie
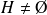de
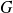est un sous-groupe de
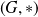si la restriction de la loi
à
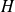munit
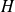d'une structure de groupe.
Une partie
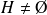de
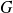est un sous-groupe de
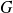si et seulement si :
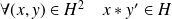(où
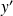est le symétrique de
).
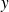Un sous-groupe
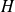d'un groupe
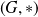est un sous-groupe distingué si :
.
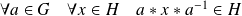Fondamental :
Toute intersection de sous-groupes de
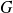est un sous-groupe de
.
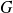L'intersection
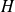de tous les sous-groupes contenant une partie
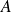de
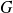est le sous-groupe engendré par
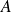(plus petit sous-groupe contenant
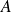). On dira que la partie
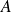est génératrice du sous-groupe
.
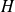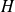est un groupe monogène s'il est engendré par un élément.
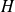est un groupe cyclique s'il est monogène et fini.
Tout groupe cyclique de cardinal
est isomorphe à
.
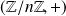Tout groupe monogène infini est isomorphe à
.
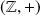Exemple :
L'ensemble des racines
èmes de l'unité dans le corps des complexes est un groupe cyclique de cardinal
.
Fondamental :
Si
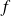est un morphisme du groupe
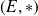vers le groupe
:
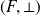L'image de l'élément neutre de
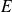est l'élément neutre de
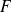.L'image du symétrique de
dans
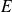est le symétrique de
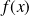dans
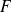.L'image d'un sous-groupe de
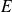est un sous-groupe de
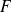.L'image réciproque d'un sous-groupe de
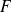est un sous-groupe de
.
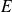Exemple :
L'application
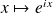est un morphisme du groupe
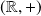dans le groupe des nombres complexes de module
muni de la multiplication.
Si
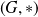est un groupe, pour tout
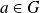, l'application qui à tout
de
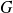associe
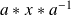est un automorphisme de
.
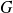