Exo 3
Commencez par chercher à résoudre l'exercice par vous-même.
Si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
Question
L'application
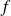 de
de
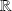 dans
dans
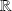 définie par :
définie par :
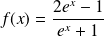 est-elle surjective ?
est-elle surjective ?
Etudiez le nombre d'antécédents d'un réel
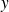 .
.
Soit un réel
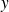 . Un réel
. Un réel
 est antécédent de
est antécédent de
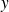 par
par
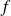 si et seulement si
si et seulement si
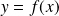 .
.
Or
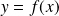 équivaut à :
équivaut à :
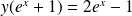 , donc à :
, donc à :
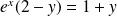 .
.
Si
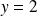 , cette équation n'a pas de solution. Donc
, cette équation n'a pas de solution. Donc
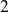 n'a pas d'antécédent par
n'a pas d'antécédent par
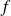 .
.
Conclusion : L'application
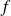 n'est pas surjective.
n'est pas surjective.
Remarque : En poursuivant la résolution, on peut montrer que
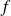 est surjective de
est surjective de
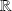 dans
dans
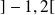 .
.
En effet, si
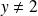 ,
,
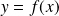 équivaut à :
équivaut à :
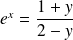 .
.
Or cette équation n'a de solution que si :
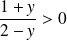 , donc si
, donc si
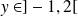 .
.
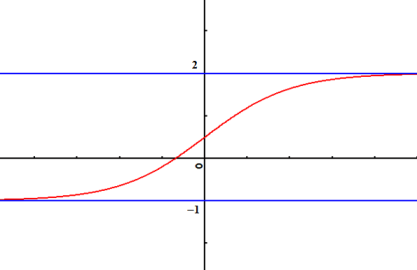
Une droite parallèle à l'axe des abscisses coupe la courbe si et seulement si son ordonnée appartient à
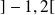 .
.





