1) Un fabricant de billes possède trois machines A, B et C qui fournissent respectivement 
, 
et 
de la production totale.
Une étude a montré que le pourcentage de billes défectueuses est de 
pour la machine A, de 
pour la machine B et de 
pour la machine C.
Après fabrication, les billes sont versées dans un bac commun aux trois machines.
On choisit au hasard une bille dans le bac.
a. Montrer que la probabilité que cette bille provienne de la machine C et soit défectueuse est
.
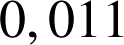b. Calculer la probabilité que cette bille soit défectueuse.
Notons
(
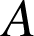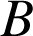ou
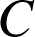) l'événement : « la bille provient de la machine A (B ou C) ».
Notons
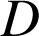l'événement : « la bille est défectueuse ».
a. 
d'où 
b. 
, réunion d'événements incompatibles deux à deux. D'après la formule des probabilités totales :
Donc 
Environ 
des billes présentent un défaut.
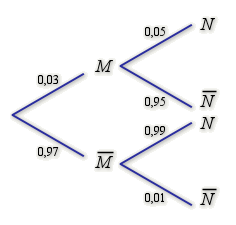
2) Une maladie atteint 
d'une population. Un test de dépistage donne les résultats suivants :
chez les individus malades,
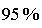des tests sont positifs,chez les individus non malades,
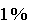des tests sont positifs.
On choisit un individu au hasard.
a. Calculer la probabilité que l'individu soit malade et que son test soit positif.
b. Calculer la probabilité que son test soit positif.
c. Donner une valeur approchée à
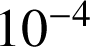près de la probabilité que l'individu soit malade alors que le test est négatif.
On note
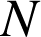l'événement : « le test est négatif » et
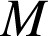l'événement : « l'individu est malade ».
a. La probabilité cherchée est 
.
b. 
.
. La probabilité que le test soit positif est
.
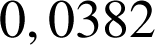c.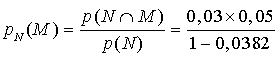 
, d'où 
.
