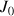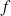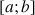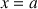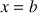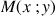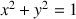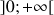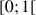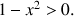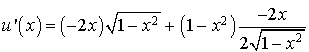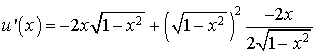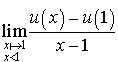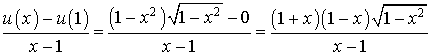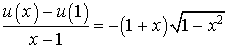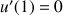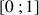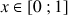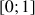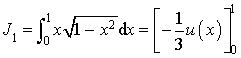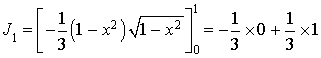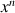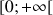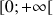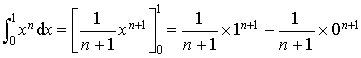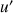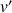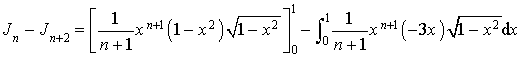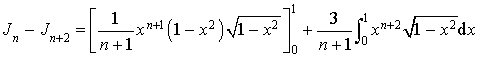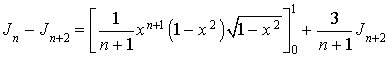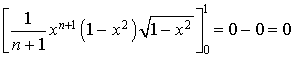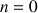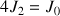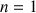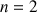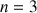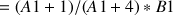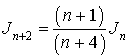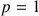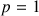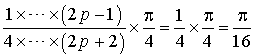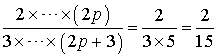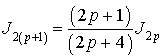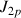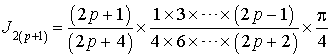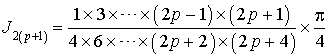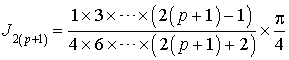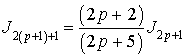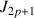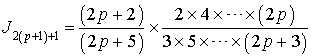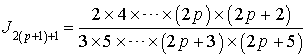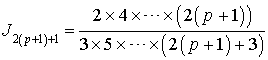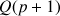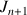Expression des termes d'une suite d'intégrales
Introduction
Prérequis : Le calcul intégral
Durée : 90 minutes
Niveau : très difficile
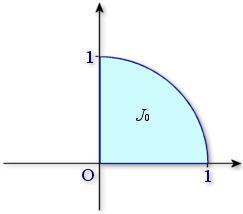
On considère la suite
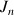 des intégrales définie par
des intégrales définie par ![]() et pour
et pour
 entier naturel non nul,
entier naturel non nul, ![]() .
.
2) Justifier que la fonction ![]() est dérivable sur
est dérivable sur
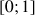 et calculer sa dérivée
et calculer sa dérivée
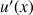 . En déduire la valeur de
. En déduire la valeur de
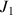 .
.
3) Démontrer que pour tout entier naturel
 non nul, on a :
non nul, on a : ![]() .
.
4) Démontrer que la suite
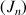 est convergente et donner sa limite.
est convergente et donner sa limite.
5) Démontrer que pour tout entier naturel
 non nul, on a :
non nul, on a : ![]() .
.
Vérifier que ce résultat reste vrai pour
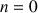 .
.
En déduire que ![]() pour tout entier naturel
pour tout entier naturel
 .
.
6) Calculer
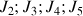 .
.
Donner, en utilisant un tableur (ou une calculatrice) des valeurs approchées des termes de la suite
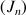 pour
pour
 variant de 0 à 20.
variant de 0 à 20.
7) Démontrer que pour tout entier naturel
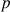 non nul, on a :
non nul, on a :
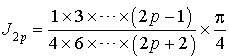 et
et 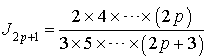 .
.
8) Démontrer que la suite
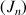 est décroissante.
est décroissante.